
分析 (1)由题意的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,则a=2b.由直线MN与圆x2+y2=$\frac{4}{5}$相切,则$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2}{\sqrt{5}}$,化为4(a2+b2)=5a2b2联立解出即可得出椭圆的标准方程.
(2)设A(x1,y1),B(x2,y2).(x1>0,x2>0),y12-1=$\frac{{x}_{1}^{2}}{4}$.设切点为Q.连接OA,OQ,在△OAQ中,丨AQ丨2=x12+y12-1=$\frac{3}{4}$x12,|AQ|=$\frac{\sqrt{3}}{2}$x1,同理,|BQ|=$\frac{\sqrt{3}}{2}$x2,|AF|=2-$\frac{\sqrt{3}}{2}$x1,|BF|=2-$\frac{\sqrt{3}}{2}$x2.即可证明△ABF的周长是定值4.切线AB⊥x轴时,把x=1代入椭圆方程解得y=$±\frac{\sqrt{3}}{2}$,可得△ABF的面积S=$\frac{1}{2}$|AB|•|$\sqrt{3}$-1|=$\frac{3-\sqrt{3}}{2}$.
切线AB与x轴不垂直时,设切线AB的方程为:my+t=x,则$\frac{|t|}{\sqrt{1+{m}^{2}}}$=1,化为:t2=1+m2.直线AB的方程与椭圆方程联立化为:(m2+4)y2+2tmy+t2-4=0,可得|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{4\sqrt{3(1+{m}^{2})}}{{m}^{2}+4}$.点F到直线AB的距离d=$\frac{|\sqrt{3}-t|}{\sqrt{1+{m}^{2}}}$.△ABF的面积S=$\frac{1}{2}$|AB|•d=$\frac{2\sqrt{3}|\sqrt{3}-t|}{{m}^{2}+4}$=$\frac{2\sqrt{3}|\sqrt{3}-t|}{{t}^{2}+3}$.(t≠0,$\sqrt{3}$).对t分类讨论,利用导数研究其单调性极值最值即可得出.
解答 解:(1)由题意的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,则a=2b,①
由直线MN与圆x2+y2=$\frac{4}{5}$相切,则$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2}{\sqrt{5}}$,化为4(a2+b2)=5a2b2,②
由①②解得:a=2,b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设A(x1,y1),B(x2,y2).(x1>0,x2>0),
∴y12-1=$\frac{{x}_{1}^{2}}{4}$.设切点为Q.
连接OA,OQ,在△OAQ中,丨AQ丨2=x12+y12-1=$\frac{3}{4}$x12,
∴|AQ|=$\frac{\sqrt{3}}{2}$x1,
同理,|BQ|=$\frac{\sqrt{3}}{2}$x2,
∴|AB|=|AQ|+|BQ|=$\frac{\sqrt{3}}{2}$(x1+x2),
∴|AB|+|AF|+|BF|=$\frac{\sqrt{3}}{2}$(x1+x2)+2-$\frac{\sqrt{3}}{2}$x1+2-$\frac{\sqrt{3}}{2}$x2=4.
∴△ABF的周长是定值4.
切线AB⊥x轴时,把x=1代入椭圆方程解得y=$±\frac{\sqrt{3}}{2}$,∴|AB|=$\sqrt{3}$,∴△ABF的面积S=$\frac{1}{2}$|AB|•|$\sqrt{3}$-1|=$\frac{3-\sqrt{3}}{2}$.
切线AB与x轴不垂直时,设切线AB的方程为:my+t=x,则$\frac{|t|}{\sqrt{1+{m}^{2}}}$=1,化为:t2=1+m2.
直线AB的方程与椭圆方程联立$\left\{\begin{array}{l}{my+t=x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,化为:(m2+4)y2+2tmy+t2-4=0,
△>0,∴y1+y2=$\frac{-2tm}{{m}^{2}+4}$,y1•y2=$\frac{{t}^{2}-4}{{m}^{2}+4}$,
∴|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{(1+{m}^{2})[\frac{4{t}^{2}{m}^{2}}{({m}^{2}+4)^{2}}-\frac{4({t}^{2}-4)}{{m}^{2}+4}]}$=$\frac{4\sqrt{3(1+{m}^{2})}}{{m}^{2}+4}$.
点F到直线AB的距离d=$\frac{|\sqrt{3}-t|}{\sqrt{1+{m}^{2}}}$.
∴△ABF的面积S=$\frac{1}{2}$|AB|•d=$\frac{2\sqrt{3}|\sqrt{3}-t|}{{m}^{2}+4}$=$\frac{2\sqrt{3}|\sqrt{3}-t|}{{t}^{2}+3}$.(t≠0,$\sqrt{3}$).
当t$>\sqrt{3}$时,S=$\frac{2\sqrt{3}(t-\sqrt{3})}{{t}^{2}+3}$,S′=$\frac{-2\sqrt{3}({t}^{2}-2\sqrt{3}t-3)}{({t}^{2}+3)^{2}}$=$\frac{-2\sqrt{3}[t-(\sqrt{3}-\sqrt{6})][t-(\sqrt{3}+\sqrt{6})]}{({t}^{2}+3)^{2}}$,
可知:t=$\sqrt{3}+\sqrt{6}$时,S取得最大值$\sqrt{2}$-1.可知:$\sqrt{2}$-1<$\frac{3-\sqrt{3}}{2}$.
当t<$\sqrt{3}$(t≠0)时,S=-$\frac{2\sqrt{3}(t-\sqrt{3})}{{t}^{2}+3}$,S′=$\frac{2\sqrt{3}[t-(\sqrt{3}+\sqrt{6})][t-(\sqrt{3}-\sqrt{6})]}{({t}^{2}+3)^{2}}$.
可知:t=$\sqrt{3}$-$\sqrt{6}$时,S取得最大值$\sqrt{2}$+1.可知:$\sqrt{2}$+1>$\frac{3-\sqrt{3}}{2}$.
可知:此时内切圆的半径r最大,由$\frac{1}{2}$×4r=$\sqrt{2}$+1,可得r=$\frac{\sqrt{2}+1}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、三角形面积计算公式、点到直线的距离公式、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
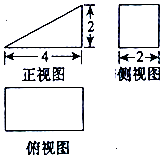
| A. | $20+4\sqrt{5}$ | B. | $12+4\sqrt{5}$ | C. | $20+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
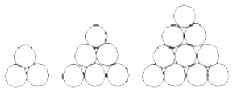 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com