
(本小题满分12分)在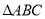 中,设角
中,设角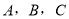 的对边分别为
的对边分别为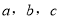 ,且
,且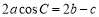 .
.
(1)求角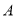 的大小;
的大小;
(2)若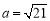 ,
,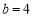 ,求边
,求边 的大小.
的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a为常数,e为自然对数的底,e≈2.71828).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)>0在区间(0,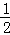 )上恒成立,求a的最小值.
)上恒成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
已知双曲线C: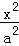 ﹣
﹣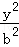 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为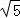 ,则C的渐近线方程为( )
,则C的渐近线方程为( )
A.y=±2x B.y=±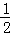 x C.y=±
x C.y=± x D.y=±
x D.y=±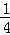 x
x
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)设函数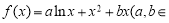 R
R ,且
,且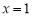 为
为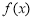 的极值点.
的极值点.
(1)当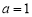 时,求
时,求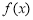 的单调递减区间;
的单调递减区间;
(2)若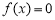 恰有两解,试求实数
恰有两解,试求实数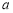 的取值范围;
的取值范围;
(3)在(1)的条件下,设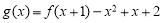 ,证明:
,证明: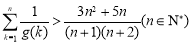 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考理科数学试卷(解析版) 题型:选择题
设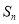 是等差数列
是等差数列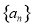 的前
的前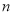 项和,已知
项和,已知 49,则
49,则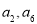 的等差中项是
的等差中项是
A.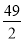 B.7 C.
B.7 C.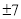 D.
D.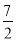
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟文科数学试卷(解析版) 题型:选择题
某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是
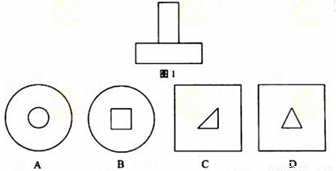
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已知函数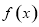 定义域
定义域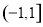 ,满足
,满足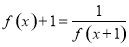 ,当
,当 时,
时,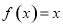 ,若函数
,若函数 ,方程
,方程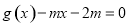 有三个实根,则实数
有三个实根,则实数 的取值范围是( )
的取值范围是( )
A.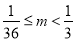 B.
B.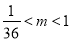 C.
C.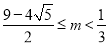 D.
D.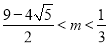
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com