
(12分)已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a为常数,e为自然对数的底,e≈2.71828).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)>0在区间(0,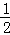 )上恒成立,求a的最小值.
)上恒成立,求a的最小值.
(1)f(x)的单调减区间为(0,2],单调增区间为(2,+∞);
(2)a的最小值为2﹣4ln2.
【解析】
试题分析:(1)先求函数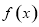 的导数
的导数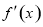 ,然后用导数
,然后用导数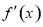 求函数
求函数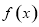 的单调区间;
的单调区间;
(2)对任意的x∈(0,),f(x)>0恒成立,即对x∈(0, ),a>2﹣
),a>2﹣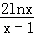 恒成立,令g(x)=2﹣
恒成立,令g(x)=2﹣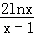 ,x∈(0,
,x∈(0, ),问题转化为求函数的
),问题转化为求函数的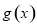 最值问题.
最值问题.
试题解析:【解析】
(1)当a=1时,f(x)=x﹣1﹣2lnx,则f′(x)=1﹣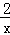 ,
,
由f′(x)>0,x>2;f′(x)<0,得0<x<2.
故f(x)的单调减区间为(0,2],单调增区间为(2,+∞);
(2)对任意的x∈(0,),f(x)>0恒成立,即对x∈(0, ),a>2﹣
),a>2﹣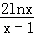 恒成立,
恒成立,
令g(x)=2﹣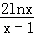 ,x∈(0,
,x∈(0, ),
),
则g′(x)=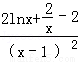 ,
,
再令h(x)=21nx+ ﹣2,x∈(0,
﹣2,x∈(0, ),则h′(x)=
),则h′(x)=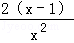 <0,
<0,
故h(x)在(0,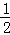 )上为减函数,
)上为减函数,
于是h(x)>h(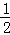 )=2﹣2ln2>0,
)=2﹣2ln2>0,
从而,g′(x)>0,于是g (x)在(0,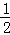 )上为增函数,
)上为增函数,
所以g(x)<g(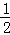 )=2﹣41n2,
)=2﹣41n2,
故要使a>2﹣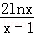 恒成立,只需a≥2﹣41n2.
恒成立,只需a≥2﹣41n2.
∴a的最小值为2﹣4ln2.
考点:1、导数在研究函数性质中的应用;2、等价转化的思想.


科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数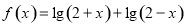 .
.
(1)求函数 的定义域;
的定义域;
(2)若不等式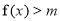 有解,求实数
有解,求实数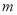 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省濮阳市高三上学期期末摸底考试理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如右图所示,则该几何体的体积为( )

A. B.
B.
C.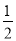 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:填空题
若函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是单调增函数,如果实数t满足f(t)+f(﹣t)<2f(1),那么t的取值范围是 _________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:选择题
设函数f(x)=sin(2x+ ),则下列结论正确的是( )
),则下列结论正确的是( )
A.f(x)的图象关于直线x= 对称
对称
B.f(x)的图象关于点( ,0)对称
,0)对称
C.f(x)的最小正周期为π
D.f(x)在[0, ]上为增函数
]上为增函数
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:填空题
将a,b都是整数的点(a,b)称为整点,若在圆x2+y2﹣6x+5=0内的整点中任取一点M,则点M到直线2x+y﹣12=0的距离大于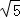 的概率为 _________ .
的概率为 _________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在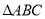 中,设角
中,设角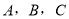 的对边分别为
的对边分别为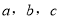 ,且
,且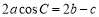 .
.
(1)求角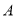 的大小;
的大小;
(2)若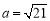 ,
,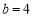 ,求边
,求边 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com