
若正三棱锥底面边长为1,侧棱与底面所成的角为![]() ,则其体积为 .
,则其体积为 .
考点:
棱柱、棱锥、棱台的体积.
专题:
计算题;空间位置关系与距离.
分析:
欲求正三棱锥的体积,先求正三棱锥的高,由题意,顶点在底面中的射影是底面的中心,从而利用侧棱与底面所成角为45°角,可求高,从而得解
解答:
解:先求正三棱锥的高,由题意,顶点P在底面中的射影是底面的中心O,
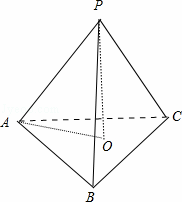
∠PAO为侧棱与底面所成角,∠PAO=45°,
从而有高PO=OA=![]() =
=![]()
又底面积S△ABC=![]() ×1=
×1=![]()
∴正三棱锥的体积V=![]() =
=![]()
故答案为:![]()
点评:
本题主要考查棱锥,线面关系、直线与平面所成的角、点到面的距离等基本知识,同时考查空间想象能力和推理、运算能力.在立体几何中,求点到平面的距离是一个常见的题型,同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com