
分析 (Ⅰ)根据a1=1,d=2,且$\frac{1}{a_1^2}$,$\frac{1}{a_4^2}$,$\frac{1}{a_m^2}$成等比数列,建立方程,即可求正整数m的值;
(Ⅱ)假设存在正整数n∈N*,使$\frac{1}{a_n},\frac{1}{{{a_{n+1}}}},\frac{1}{{{a_{n+2}}}}$成等差数列,证明d=0,与已知d>0矛盾,故假设不成立,从而对任意n∈N*,$\frac{1}{a_n}$,$\frac{1}{{{a_{n+1}}}}$,$\frac{1}{{{a_{n+2}}}}$都不成等差数列.
解答 (Ⅰ)解:a4=7,am=2m-1,∴$1•\frac{1}{{{{(2m-1)}^2}}}={(\frac{1}{7^2})^2}$,∴2m-1=49,m=25,
(Ⅱ)证明:假设存在正整数n∈N*,使$\frac{1}{a_n},\frac{1}{{{a_{n+1}}}},\frac{1}{{{a_{n+2}}}}$成等差数列,
则$\frac{2}{{{a_{n+1}}}}=\frac{1}{a_n}+\frac{1}{{{a_{n+2}}}}$,即$\frac{2}{{{a_{n+1}}}}=\frac{1}{{{a_{n+1}}-d}}+\frac{1}{{{a_{n+1}}+d}}=\frac{{2{a_{n+1}}}}{{a_{_{n+1}}^2-{d^2}}}$,
∴d=0,这与已知d>0矛盾,故假设不成立,原结论成立.
点评 本题考查等差数列、等比数列的性质,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<2 } | B. | {x|0<x<2} | C. | {x|0≤x<l} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4}$ | B. | $\frac{π}{2}$-4 | C. | $\frac{π-1}{4}$ | D. | $\frac{π-4}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
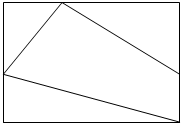 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充分必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com