
已知四棱锥P-ABCD的正视图是一个底边长为4,腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.

(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
(1)见解析(2)6
【解析】(1)证明:依题意,可知点P在平面ABCD上的正射影是线段CD的中点E,连接PE,则PE⊥平面ABCD.
∵AD?平面ABCD,
∴AD⊥PE.
∵AD⊥CD,CD∩PE=E,CD?平面PCD,PE?平面PCD,
∴AD⊥平面PCD.
∵PC?平面PCD,
∴AD⊥PC.
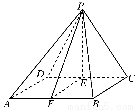
(2)依题意,在等腰三角形PCD中, PC=PD=3,DE=EC=2,
在Rt△PED中,PE= .
.
过点E作EF⊥AB,垂足为F,连接PF,
∵PE⊥平面ABCD,AB?平面ABCD,
∴AB⊥PE.
∵EF?平面PEF,PE?平面PEF,EF∩PE=E,
∴AB⊥平面PEF.
∵PF?平面PEF,
∴AB⊥PF,
依题意得EF=AD=2.
在Rt△PEF中,PF=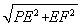 =3,
=3,
∴△PAB的面积为S=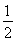 ·AB·PF=6.
·AB·PF=6.
∴四棱锥P-ABCD的侧面PAB的面积为6.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:选择题
某师傅需用合板制作一个工作台,工作台由主体和附属两部分组成,主体部分全封闭,附属部分是为了防止工件滑出台面而设置的三面护墙,其大致形状的三视图如图所示(单位长度: cm), 则按图中尺寸,做成的工作台用去的合板的面积为(制作过程合板的损耗和合板厚度忽略不计)( )

A.40 000 cm2 B.40 800 cm2
C.1600(22+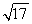 )cm2 D.41 600 cm2
)cm2 D.41 600 cm2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
已知函数f(x)=|2x-a|+a.若不等式f(x)≤6的解集为{x|-2≤x≤3},则实数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E,F,点M在EF上,且∠BAD=∠BMF.
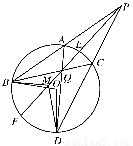
(1)求证:PA·PB=PM·PQ;
(2)求证:∠BMD=∠BOD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,在正△ABC中,点D,E分别在边BC,AC上,且BD=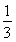 BC,CE=
BC,CE=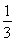 CA,AD,BE相交于点P,求证:
CA,AD,BE相交于点P,求证:
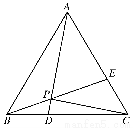
(1)P,D,C,E四点共圆;
(2)AP⊥CP.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
已知数列{an}的相邻两项an,an+1是关于x的方程x2-2nx+bn=0的两根,且a1=1.
(1)求证:数列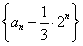 是等比数列;
是等比数列;
(2)求数列{an}的前n项和Sn;
(3)设函数f(n)=bn-t·Sn(n∈N*),若f(n)>0对任意的n∈N*都成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:解答题
如果对任意实数x,y,都有f(x+y)=f(x)·f(y),且f(1)=2,
(1)求f(2),f(3),f(4)的值.
(2)求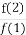 +
+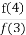 +
+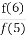 +…+
+…+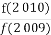 +
+ +
+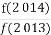 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:填空题
函数y=f(x)(x∈R)有下列命题:
①在同一坐标系中,y=f(x+1)与y=f(-x+1)的图象关于直线x=1对称;
②若f(2-x)=f(x),则函数y=f(x)的图象关于直线x=1对称;
③若f(x-1)=f(x+1),则函数y=f(x)是周期函数,且2是一个周期;
④若f(2-x)=-f(x),则函数y=f(x)的图象关于(1,0)对称,其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:选择题
已知函数f(x)=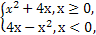 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )
(A)(-∞,-1)∪(2,+∞)
(B)(-1,2)
(C)(-2,1)
(D)(-∞,-2)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com