练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若直线l：ax＋by＋4＝0(a>0，b>0)始终平分圆C：x2＋y2＋8x＋2y＋1＝0，则ab的最大值为________．


    1

    解析：圆C的圆心坐标为(－4，－1)，则有－4a－b＋4＝0，即4a＋b＝4.所以ab＝(4ab)≤＝1.当且仅当a＝，b＝2取得等号．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知船在灯塔北偏东处，且船到灯塔的距离为2，船在灯塔北偏西处，两船间的距离为，则船到灯塔的距离为        ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过点（0，1）作曲线y=lnx的切线，则切线方程为________________________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知t∈R，圆C：x2＋y2－2tx－2t2y＋4t－4＝0.

    (1) 若圆C的圆心在直线x－y＋2＝0上，求圆C的方程；

    (2) 圆C是否过定点？如果过定点，求出定点的坐标；如果不过定点，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    P(x，y)在圆C：(x－1)2＋(y－1)2＝1上移动，试求x2＋y2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


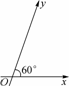
    如图，在平面斜坐标系xOy中，∠xOy＝60°，平面上任一点P关于斜坐标系的斜坐标是这样定义的：若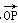＝xe1＋ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量)，则P点斜坐标为(x，y)．

    (1) 若P点斜坐标为(2，－2)，求P到O的距离|PO|；

    (2) 求以O为圆心，1为半径的圆在斜坐标系xOy中的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题：

    ①若l与m为异面直线，l⊂α，m⊂β，则α∥β； ②若α∥β，l⊂α，m⊂β，则l∥m；

    ③若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.

    其中真命题的个数为                   (　　)

    A.3　　　　    B.2　　　　    C.1　　　　    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


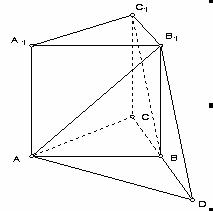
    如图，正三棱柱ABC—A1B1C1的底面边长的3，侧棱AA1=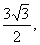D是CB延长线上一点，且BD=BC.

       （Ⅰ）求证：直线BC1//平面AB1D；

       （Ⅱ）求二面角B1—AD—B的大小；

       （Ⅲ）求三棱锥C1—ABB1的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数.

    （1）求函数在上的最小值；

    （2）设，若对任意，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案