
(满分16分)
记函数f(x)的定义域为D,若存在 ,使
,使 成立,则称以
成立,则称以 为坐标的点为函数
为坐标的点为函数 图象上的不动点。
图象上的不动点。
(1)若函数 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明
(1)
(2)证明略
解析解:(1)由 , …………………………………………2分
, …………………………………………2分
整理得  ……………………………………4分
……………………………………4分
由题意知方程(*)有两个互为相反数的根,所以 即
即 ………6分
………6分 ,
, ,……………………………………………………8分
,……………………………………………………8分
故 应满足
应满足 且
且 ……………………………………………………10分
……………………………………………………10分
(2)结论正确。……………………………………………………12分
证明: 为奇函数,
为奇函数, ,取
,取 ,得
,得 ,
,
即(0,0)为函数的一个不动点,设函数 除0以外还有不动点
除0以外还有不动点 ,
,
则
又 ,故
,故 也为函数的不动点。…………………14分
也为函数的不动点。…………………14分
综上,若定义在R上的奇函数 图象上存在有限个不动点,则不动点有奇数个。
图象上存在有限个不动点,则不动点有奇数个。
例如: 。…………………………………………………16分
。…………………………………………………16分


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
(本题满分15分)
已知:函数 (a、b、c是常数)是奇函数,且满足
(a、b、c是常数)是奇函数,且满足 .
.
(1)求a、b、c的值;
(2)试判断函数f(x)在区间(0, )上的单调性并证明.
)上的单调性并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
医学上为研究某种传染病传播过程中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞在体内的总数与天数的关系记录如下表.已知该种病毒细胞在小白鼠体内的个数超过 的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的
的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的 .
.
(Ⅰ) 为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)
(Ⅱ)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)
(参考数据: ,
, )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数f(x)= (x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为
(x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为 。
。
(1)求证P的纵坐标为定值; (4分)
(2)若数列{ }的通项公式为
}的通项公式为 =f(
=f( )(m∈N
)(m∈N ,n=1,2,3,…,m),求数列{
,n=1,2,3,…,m),求数列{ }的前m项和
}的前m项和 ; (5分)
; (5分)
(3)若m∈N 时,不等式
时,不等式
 <
< 横成立,求实数a的取值范围。(3分)
横成立,求实数a的取值范围。(3分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数

(1)判断 的奇偶性并证明;
的奇偶性并证明;
(2)若 的定义域为[
的定义域为[ ](
]( ),判断
),判断 在定义域上的增减性,并加以证明;
在定义域上的增减性,并加以证明;
(3)若 ,使
,使 的值域为[
的值域为[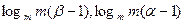 ]的定义域区间[
]的定义域区间[ ](
]( )是否存在?若存在,求出[
)是否存在?若存在,求出[ ],若不存在,请说明理由.
],若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本大题满分12分)
某公司预计全年分批购入每台价值为2 000元的电视机共3600台,每批都购入x台
000元的电视机共3600台,每批都购入x台 ,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰
,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰 当安排每批进货的数量,使资金够用?写出你的结论并说明理由
当安排每批进货的数量,使资金够用?写出你的结论并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com