
(本大题满分12分)
某公司预计全年分批购入每台价值为2 000元的电视机共3600台,每批都购入x台
000元的电视机共3600台,每批都购入x台 ,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰
,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰 当安排每批进货的数量,使资金够用?写出你的结论并说明理由
当安排每批进货的数量,使资金够用?写出你的结论并说明理由
科目:高中数学 来源: 题型:解答题
(本题满分16分)
已知函数 (
( ∈R且
∈R且 ),
), .
.
(Ⅰ)若 ,且函数
,且函数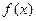 的值域为[0, +
的值域为[0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时, 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设 ,
, , 且
, 且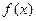 是偶函数,判断
是偶函数,判断 能否大于零?
能否大于零?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(满分16分)
记函数f(x)的定义域为D,若存在 ,使
,使 成立,则称以
成立,则称以 为坐标的点为函数
为坐标的点为函数 图象上的不动点。
图象上的不动点。
(1)若函数 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 接近
接近 .
.
(1)若 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、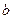 ,证明:
,证明: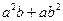 比
比 接近
接近 ;
;
(3)已知函数 的定义域
的定义域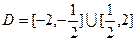 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最值和单调性(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知函数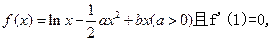
(I)试用含a的式子表示b,并求函数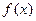 的单调区间;
的单调区间;
(II)已知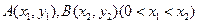 为函数
为函数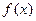 图象上不同两点,
图象上不同两点,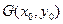 为AB的中点,记A、B两点连线的斜率为k,证明:
为AB的中点,记A、B两点连线的斜率为k,证明: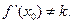
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com