
分析 根据条件得出4y=1-(3x)2,运用指数幂得出m=3x-1+22y-1=$\frac{1}{3}$×3x+$\frac{1}{2}×$4x=$\frac{1}{3}×{3}^{x}$$+\frac{1}{2}×$(1-(3x)2)=-$\frac{1}{2}×$(3x)2$+\frac{1}{3}×{3}^{x}$$+\frac{1}{2}$,整体转化为二次函数求解即可.
解答 解:∵9x+4y=1,
∴4y=1-(3x)2,
∴m=3x-1+22y-1=$\frac{1}{3}$×3x+$\frac{1}{2}×$4x=$\frac{1}{3}×{3}^{x}$$+\frac{1}{2}×$(1-(3x)2)=-$\frac{1}{2}×$(3x)2$+\frac{1}{3}×{3}^{x}$$+\frac{1}{2}$
设t=3x,
∴m=$-\frac{1}{2}{t}^{2}$$+\frac{1}{3}t$$+\frac{1}{2}$,
当t=$\frac{1}{3}$时,m最大值为:$-\frac{1}{2}×\frac{1}{9}$$+\frac{1}{9}$$+\frac{1}{2}$=$\frac{10}{18}$=$\frac{5}{9}$
点评 本题考查了运用函数思想转化求解代数式的范围问题,属于中档题,关键是指数幂的化简运算.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,6)) | B. | (3,6) | C. | (-6,3)) | D. | [-3,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的单调递减区间为[2n-3,2n-2](n∈N*) | |
| B. | f(x)的值域为[0,+∞) | |
| C. | 方程f(x)=1在区间[-2,2n]上所有根的个数为2n+1(n∈N) | |
| D. | 若方程f(x)=x+2在区间[-2,4]内有3个不等实根,则实数的取值范围是-2<a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
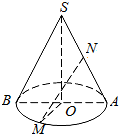 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com