
设定义在(0,+∞)上的函数f(x)=ax+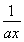 +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y=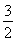 x,求a,b的值.
x,求a,b的值.
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知双曲线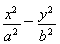 =1和椭圆
=1和椭圆 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角或钝角三角形
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
在等差数列{an}中,首项a1=120,公差d=-4,若Sn≤an(n≥2),则n的最小值为( )
A.60 B.62 C.70 D.72
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷2练习卷(解析版) 题型:选择题
将函数y=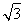 cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
A.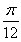 B.
B.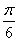 C.
C.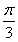 D.
D. 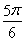
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
已知函数f(x)=ax2-ln x,x∈(0,e],其中e是自然对数的底数,a∈R.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)是否存在实数a,使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:填空题
函数g(x)=x2-2 013x,若g(a)=g(b),a≠b,则g(a+b)=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
若a,b∈R,且ab>0,则下列不等式中,恒成立的是( )
A.a+b≥2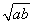 B.
B.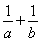 >
>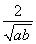
C.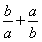 ≥2 D.a2+b2>2ab
≥2 D.a2+b2>2ab
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
已知函数f(x)=-x3+x2,g(x)=aln x,a∈R.
(1)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范围;
(2)设F(x)=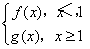 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练D组练习卷(解析版) 题型:填空题
设四面体的六条棱的长分别为1,1,1,1,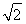 和a且长为a的棱与长为
和a且长为a的棱与长为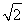 的棱异面,则a的取值范围是________.
的棱异面,则a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com