
 ij��Ϊ�˹��������Լ��ˮ��ʵ�С�����ʽ��ˮ�ۣ�������ÿ�����������ˮ������Ϊ����������ˮ��������4�ֵIJ��ְ�2Ԫ/���շѣ�����4�ֵ�������8�ֵIJ��ְ�4Ԫ/���շѣ�����8�ֵIJ��ְ�8Ԫ/���շѣ�
ij��Ϊ�˹��������Լ��ˮ��ʵ�С�����ʽ��ˮ�ۣ�������ÿ�����������ˮ������Ϊ����������ˮ��������4�ֵIJ��ְ�2Ԫ/���շѣ�����4�ֵ�������8�ֵIJ��ְ�4Ԫ/���շѣ�����8�ֵIJ��ְ�8Ԫ/���շѣ����� ��1�������⣬���÷ֶκ��������ʼ������y��x�ĺ�������ʽ��
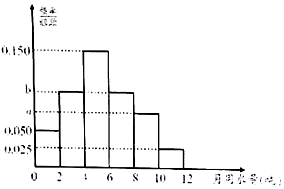
��2�����Ƶ�ʷֲ�ֱ��ͼ��֪��$\left\{{\begin{array}{l}{0.1+2b+0.3=0.6}\\{2b+2a+0.05=0.4}\end{array}}\right.$���������a��b��ֵ��
��3��Y�Ŀ���ȡֵΪ1��3��5��7��9��11���ֱ���ø��ʣ�������ѧ������ʽ�������Y����ѧ������
��� �⣺��1����0��x��4ʱ��y=2x��
��4��x��8ʱ��y=2��4+4����x-4��=4x-8��
��x��8ʱ��y=2��4+4��4+8����x-8��=8x-40��
����y��x֮��ĺ�������ʽΪ��$y=\left\{{\begin{array}{l}{2x��0��x��4}\\{4x-8��4��x��8}\\{8x-40��x��8}\end{array}}\right.$��
��2���ɣ�1����֪����y=16ʱ��x=6����P��x��6��=0.60��
���Ƶ�ʷֲ�ֱ��ͼ��֪��$\left\{{\begin{array}{l}{0.1+2b+0.3=0.6}\\{2b+2a+0.05=0.4}\end{array}}\right.$��
��a=0.075��b=0.1��
��3���������֪��Y�Ŀ���ȡֵΪ1��3��5��7��9��11��
��P��Y=1��=0.1��P��Y=3��=0.2��P��Y=5��=0.3��P��Y=7��=0.2��P��Y=9��=0.15��P��Y=11��=0.05��
����P�ķֲ��У�
| P | 1 | 3 | 5 | 7 | 9 | 11 |
| Y | 0.1 | 0.2 | 0.3 | 0.2 | 0.15 | 0.05 |
���� ���⿼��ֶκ����ļ�Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�����ֲ��м���ѧ��������������������������е��⣮


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��������x��Ԫ�� | 4 | 5 | 6 | 7 | 8 | 9 |
| ��Ʒ����y������ | q | 84 | 83 | 80 | 75 | 68 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{7}{2}$ | B�� | $\frac{9}{2}$ | C�� | $\frac{7}{2}$ | D�� | $-\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2x | B�� | $y=\frac{1}{2}x$ | C�� | y=��2x | D�� | $y=��\frac{1}{2}x$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
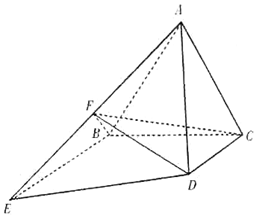 ��ͼ��ʾ����������ABC����ƽ��������BCDE����ƽ�洹ֱ��BE��CD��BE=2CD=4��BE��BC��FΪ��AB���е㣮
��ͼ��ʾ����������ABC����ƽ��������BCDE����ƽ�洹ֱ��BE��CD��BE=2CD=4��BE��BC��FΪ��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��8�� | B�� | ��2��16�� | C�� | ��4��8�� | D�� | $��2\sqrt{2}��16��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2$\sqrt{2}$ | B�� | -$\sqrt{2}$ | C�� | 0 | D�� | 2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com