
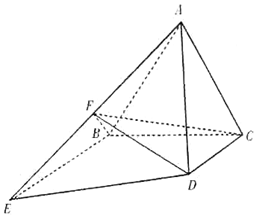
 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.分析 (1)推导出BE⊥平面ABC,从而BE⊥CF,再求出CF⊥AB,由此能证明CF⊥平面ABE.
(2)取BC中点G,连接AG,由VD-BEF=VF-BDE,能求出三棱锥D-BEF的体积.
解答 证明:(1)∵平面ABC⊥平面BCDE,
平面ABC∩平面BCDE=BC,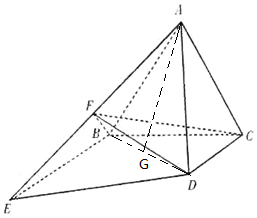
且BE?平面BCDE,BE⊥BC,
∴BE⊥平面ABC,
∴BE⊥CF,
又∵△ABC为正三角形,F为AB的中点,
∴CF⊥AB,
又∵BE、AB?平面ABE,BE∩AB=B,
∴CF⊥平面ABE;
解:(2)取BC中点G,连接AG,
由题意知CD⊥平面ABC,
∴DA与平面ABC所成的角为∠DAC=30°,
∵Rt△ACD中,CD=2,∴$AD=4,AC=2\sqrt{3}$,
∵△ABC为正三角形,G为BC的中点,
∴AG⊥BC且$AG=3,BC=2BG=2\sqrt{3}$,
∵平面ABC⊥平面BCDE,∴AG⊥平面BCDE,
又∵F为AB的中点,∴点F到平面BCDE的距离为$\frac{1}{2}AG=\frac{3}{2}$,
∵$BE⊥BC,BE=4,BC=2\sqrt{3}$,
∴${S_{△BDE}}=\frac{1}{2}•BE•BC=4\sqrt{3}$,
∴${V_{D-BEF}}={V_{F-BDE}}=\frac{1}{3}•{S_{△BDE}}•\frac{1}{2}AG=\frac{1}{3}•4\sqrt{3}•\frac{3}{2}=2\sqrt{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、空间思维能力、运算求解能力,考查等价转化思想、数形结合思想,是中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+y2=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,且m、n是异面直线,那么n与α相交 | |
| B. | 若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β | |
| C. | 若m?α,n?α,且m∥β,n∥β,则α∥β | |
| D. | 若m∥α,n∥β,且α∥β,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
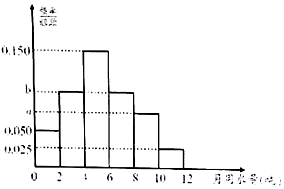 某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
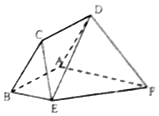 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com