
分析 (Ⅰ)由题意,|x-2|>|2x+1|.两边平方,不等式可化为3x2+8x-3<0,即可求不等式f(x)>0的解集;
(Ⅱ)若?x0∈R,使得f(x0)>2m+1,等价于f(x)max>2m+1,即可求实数m的取值范围.
解答 解:(Ⅰ)由题意,|x-2|>|2x+1|.
两边平方,不等式可化为3x2+8x-3<0,解得-3$<x<\frac{1}{3}$,
∴不等式的解集为(-3,$\frac{1}{3}$);
(Ⅱ)?x0∈R,使得f(x0)>2m+1,等价于f(x)max>2m+1,
∵f(x)=$\left\{\begin{array}{l}{x+3,x<-\frac{1}{2}}\\{-3x+1,-\frac{1}{2}≤x≤2}\\{-x-3,x>2}\end{array}\right.$,∴f(x)max=f(-$\frac{1}{2}$)=$\frac{5}{2}$
∴$\frac{5}{2}$>2m+1,
∴m<$\frac{3}{4}$.
点评 本题考查绝对值不等式,考查存在性问题,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,且m、n是异面直线,那么n与α相交 | |
| B. | 若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β | |
| C. | 若m?α,n?α,且m∥β,n∥β,则α∥β | |
| D. | 若m∥α,n∥β,且α∥β,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
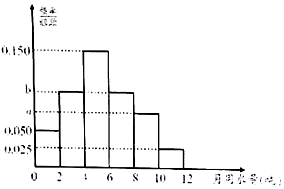 某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
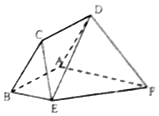 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com