
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
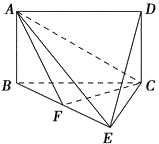
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上.若DE∥平面ACF,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是边长
是边长![]() ,
,![]() 的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,
的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,![]() 、
、![]() 是
是![]() 上被切去的小正方形的两个顶点,设
上被切去的小正方形的两个顶点,设![]() .
.

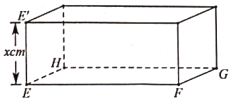
(1)将长方体盒子体积![]() 表示成
表示成![]() 的函数关系式,并求其定义域;
的函数关系式,并求其定义域;
(2)当![]() 为何值时,此长方体盒子体积
为何值时,此长方体盒子体积![]() 最大?并求出最大体积.
最大?并求出最大体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点
,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点![]() 不含端点A,B,
不含端点A,B,![]() ,且
,且![]() ,则
,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种智能手机的投入成本是4500元/部,当手机售价为6000元/部时,月销售量为![]() 台,市场分析的结果表明,如果手机的销售价提高的百分率为
台,市场分析的结果表明,如果手机的销售价提高的百分率为![]() ,那么月销售量减少的百分率为
,那么月销售量减少的百分率为![]() .记销售价提高的百分率为
.记销售价提高的百分率为![]() 时,月利润是
时,月利润是![]() 元.
元.
(1)写出月利润![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何确定这种智能手机的销售价,使得该公司的月利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com