
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;
;
(2)随机变量![]() 的分布列为:
的分布列为:
|
| 10 | 20 | 30 | 40 |
|
|
|
|
|
|
![]() .
.
【解析】
试题(1)这属于一个古典概型问题,可以考虑摸2次,总的方法数为![]() ,而摸2次后停止摸奖,说明第一次不是黑球,而第2次摸的是黑球,有
,而摸2次后停止摸奖,说明第一次不是黑球,而第2次摸的是黑球,有![]() 种可能,因此所求概率为
种可能,因此所求概率为![]() ;(2)因为是不放回的摸球,因此得奖金额可能为0元、10元、20元、30元、40元,这样随机变量
;(2)因为是不放回的摸球,因此得奖金额可能为0元、10元、20元、30元、40元,这样随机变量![]() 的分布列就要求出,奖金0元,说明第1次摸的是黑球,奖金10元说明第一次摸的是拍球或黄球,第2次黑球,奖金20元,说明第1次红球,第2次黑球或第1、第2次是白球或黄球,第3次黑球,奖金30元,第1次与第2次里有1次是红球,另一次为白球或黄球,第3次黑球,而奖金40元说明第4次是黑球,由上可计算出名概率计算出分布列,期望.
的分布列就要求出,奖金0元,说明第1次摸的是黑球,奖金10元说明第一次摸的是拍球或黄球,第2次黑球,奖金20元,说明第1次红球,第2次黑球或第1、第2次是白球或黄球,第3次黑球,奖金30元,第1次与第2次里有1次是红球,另一次为白球或黄球,第3次黑球,而奖金40元说明第4次是黑球,由上可计算出名概率计算出分布列,期望.
试题解析:(1)设“1名顾客摸球2次停止摸奖”为事件![]() ,
,
则![]() ,(4分)
,(4分)
故1名顾客摸球2次停止摸奖的概率![]() .
.
(2)随机变量![]() 的所有取值为
的所有取值为![]() .
.
![]() ,
,![]() ,
,![]()
![]() ,
,![]() (9分)
(9分)
所以,随机变量![]() 的分布列为:
的分布列为:
|
| 10 | 20 | 30 | 40 |
|
|
|
|
|
|
(12分)
![]() .(14分)
.(14分)


科目:高中数学 来源: 题型:
【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
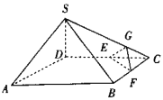
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
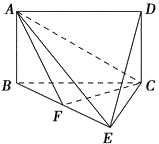
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上.若DE∥平面ACF,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)讨论f(x)的单调性;
(2)函数g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com