
【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)第5天时的销售利润最大,最大值2025元.(3)
(2)第5天时的销售利润最大,最大值2025元.(3)![]()
【解析】
(1)若选一次函数,则设为![]() ,代
,代![]() ,
,![]() 求解,再代入其他点验证是否符合题意,若选反比例函数,则设为
求解,再代入其他点验证是否符合题意,若选反比例函数,则设为![]() ,代
,代![]() ,
,![]() 求解,再代入其他点验证是否符合题意.
求解,再代入其他点验证是否符合题意.
(2)设日销售利润为![]() 元,根据(1)的结果,分当
元,根据(1)的结果,分当![]() ,
,![]() 时,讨论求解.
时,讨论求解.
(3)建立函数模型![]() ,根据每天扣除捐赠后的日销售利润随时间
,根据每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,因为
(天)的增大而增大,因为![]() ,则由二次函数的性质,对称轴应
,则由二次函数的性质,对称轴应![]() 求解.
求解.
(1)若选一次函数,则设为![]() ,代
,代![]() ,
,![]() ,
,
得![]() ,解得
,解得![]()
所以![]() ,
,
代![]() 入
入![]() 中,符合题意;
中,符合题意;
若选反比例函数,则设为![]() ,代
,代![]() ,
,![]() ,
,
得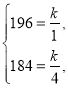 ,解得
,解得![]() ,不合题意.
,不合题意.
所以,![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
(2)设日销售利润为![]() 元,当
元,当![]() 时,
时,
![]() ,
,
所以当![]() 时,有最大值2025元.
时,有最大值2025元.
当![]() 时,
时,![]() ,
,
因当![]() 时,
时,![]() 随
随![]() 的增大而减小,故当
的增大而减小,故当![]() 时,
时,![]() 有最大值952元.
有最大值952元.
综上所述,第5天时的销售利润最大,最大值2025元.
(3)![]() ,
,
对称轴为![]() ,因为
,因为![]() ,且
,且![]() 为整数,
为整数,![]() 随
随![]() 的增大而增大,开口向下,
的增大而增大,开口向下,
所以![]() ,所以
,所以![]() ,故
,故![]() .所以
.所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的左、右焦点分别是F1,F2,焦距为2c,若直线y=
(a>b>0)的左、右焦点分别是F1,F2,焦距为2c,若直线y=![]() (x+c)与椭圆交于M点,且满足∠MF1F2=2∠MF2F1,则椭圆的离心率是 ( )
(x+c)与椭圆交于M点,且满足∠MF1F2=2∠MF2F1,则椭圆的离心率是 ( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
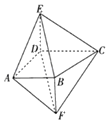
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式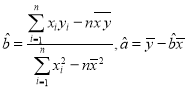 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com