
【题目】已知函数![]() ,
,![]() .
.
(1)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的右顶点和下顶点.
分别是椭圆的右顶点和下顶点.
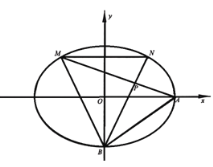
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 是椭圆
是椭圆![]() 内一点,直线
内一点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,直线
,直线![]() 分别交椭圆于
分别交椭圆于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() .
.
①若![]() 两点关于
两点关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
②证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内有![]() 个不同的红球,
个不同的红球,![]() 个不同的白球,
个不同的白球,
(1)从中任取![]() 个球,红球的个数不比白球少的取法有多少种?
个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记![]() 分,取一个白球记
分,取一个白球记![]() 分,从中任取
分,从中任取![]() 个球,使总分不少于
个球,使总分不少于![]() 分的取法有多少种?
分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com