
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数有两个零点,求满足条件的最小正整数![]() 的值.
的值.
【答案】(1) 当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)3.
;(2)3.
【解析】
(1)先求导,再对![]() 进行分类讨论,利用导数与函数的单调性的关系即可得出;
进行分类讨论,利用导数与函数的单调性的关系即可得出;
(2)由(1)可知,若函数![]() 有两个零点,则
有两个零点,则![]() ,且
,且![]() .转化为求满足
.转化为求满足![]() 的最小正整数
的最小正整数![]() 的值,利用单调性判断其零点所在的最小区间即可求得.
的值,利用单调性判断其零点所在的最小区间即可求得.
(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .所以函数
.所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由(1)可知,若函数![]() 有两个零点,则
有两个零点,则![]() ,且
,且![]() .
.
即 ,
,
即![]() ,
,
![]() .
.
令![]() ,易知
,易知![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
又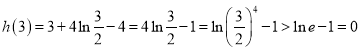 ,
,
即![]() .
.
所以存在![]() ,使
,使![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以满足![]() 的最小正整数
的最小正整数![]() 的值为3.
的值为3.
又![]() 时,
时,![]() ,且函数
,且函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
综上,满足条件的最小正整数![]() 的值为3.
的值为3.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
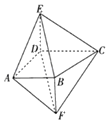
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式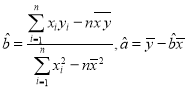 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
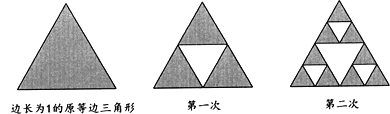
【题目】如图,将一个边长为![]() 的正三角形分成
的正三角形分成![]() 个全等的正三角形,第一次挖去中间的一个小三角形,将剩下的
个全等的正三角形,第一次挖去中间的一个小三角形,将剩下的![]() 个小正三角形,分别再从中间挖去一个小三角形,保留它们的边,重复操作以上的做法,得到的集合为希尔宾斯基三角形.设
个小正三角形,分别再从中间挖去一个小三角形,保留它们的边,重复操作以上的做法,得到的集合为希尔宾斯基三角形.设![]() 是前
是前![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第
是第![]() 次挖去的中间小三角形面积,
次挖去的中间小三角形面积,![]() 是前
是前![]() 次挖去的
次挖去的![]() 个小三角形面积之和),则
个小三角形面积之和),则![]() _____________ ,
_____________ ,![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com