
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式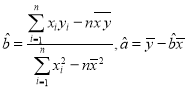 )
)
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 直线
直线![]() ,且直线
,且直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 两点和
两点和![]() 两点.
两点.
(Ⅰ)若![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且直线
的左、右焦点,且直线![]() 轴,求四边形
轴,求四边形![]() 的面积;
的面积;
(Ⅱ)若直线![]() 的斜率存在且不为0,四边形
的斜率存在且不为0,四边形![]() 为平行四边形,求证:
为平行四边形,求证:![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,判断四边形![]() 能否为矩形,说明理由.
能否为矩形,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com