
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
【答案】(1)①优等品3件,合格品2件;②![]() ;(2)选择乙生产方式.
;(2)选择乙生产方式.
【解析】
(1)①根据频数分布表知:甲的优等品率为0.6,合格品率为0.4,即可得到抽去的件数;
②记3件优等品为![]() ,
,![]() ,
,![]() ,2件合格品分别为
,2件合格品分别为![]() ,
,![]() ,从中随机抽2件,列举出基本事件的总数,利用古典概型及其概率的计算公式,即可求解;
,从中随机抽2件,列举出基本事件的总数,利用古典概型及其概率的计算公式,即可求解;
(2)分别计算出甲、乙种生产方式每生产100件所获得的利润为![]() 元
元![]() 元,比较即可得到结论。
元,比较即可得到结论。
(1)①由频数分布表知:甲的优等品率为0.6,合格品率为0.4,所以抽出的5件产品中,优等品3件,合格品2件.
②记3件优等品为![]() ,
,![]() ,
,![]() ,2件合格品分别为
,2件合格品分别为![]() ,
,![]() ,从中随机抽2件,抽取方式有
,从中随机抽2件,抽取方式有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
设“这2件中恰有1件是优等品的事件”为![]() ,则事件
,则事件![]() 发生的情况有6种,
发生的情况有6种,
所以![]() .
.
(2)根据样本知甲种生产方式生产100件农产品有60件优等品,40件合格品;乙种生产方式生产100件农产品有80件优等品,20件合格品.
设甲种生产方式每生产100件所获得的利润为![]() 元,
元,
乙种生产方式每生产100件所获得的利润为![]() 元,
元,
可得![]() (元),
(元),
![]() (元),
(元),
由于![]() ,所以用样本估计总体知乙种生产方式生产的农产品所获得的利润较高,该扶贫单位要选择乙生产方式来帮助该扶贫村来脱贫较好.
,所以用样本估计总体知乙种生产方式生产的农产品所获得的利润较高,该扶贫单位要选择乙生产方式来帮助该扶贫村来脱贫较好.


科目:高中数学 来源: 题型:
【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况,调查部门在该校进行了一次问卷调查(共12道题),从该校学生中随机抽取40人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如下频率分布直方图.
六组,得到如下频率分布直方图.
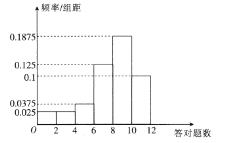
(1)若答对一题得10分,未答对不得分,估计这40人的成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)讨论f(x)的单调性;
(2)函数g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2019年,石室2160岁!文翁兴学2160周年纪念活动于2019年11月9日在石室中学文庙校区运动场隆重召开,会场是由一个长![]() ,宽
,宽![]() 的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线
的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线![]() 对称,图形如下.
对称,图形如下.
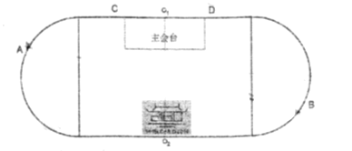
(1)若![]() 、
、![]() 两位同学分别在左右两个半圆弧上值勤,则
两位同学分别在左右两个半圆弧上值勤,则![]() 、
、![]() 两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
(2)在(1)问的情况下,若要在主会台后的会场边界上关于中轴线对称的两点![]() 、
、![]() 处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时
处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时![]() 、
、![]() 两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以
两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以![]() 秒计算,声音在空气中的传播速度为
秒计算,声音在空气中的传播速度为![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com