
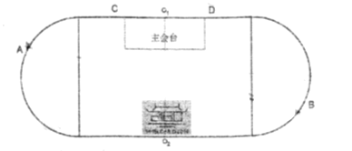
【题目】公元2019年,石室2160岁!文翁兴学2160周年纪念活动于2019年11月9日在石室中学文庙校区运动场隆重召开,会场是由一个长![]() ,宽
,宽![]() 的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线
的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线![]() 对称,图形如下.
对称,图形如下.
(1)若![]() 、
、![]() 两位同学分别在左右两个半圆弧上值勤,则
两位同学分别在左右两个半圆弧上值勤,则![]() 、
、![]() 两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
(2)在(1)问的情况下,若要在主会台后的会场边界上关于中轴线对称的两点![]() 、
、![]() 处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时
处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时![]() 、
、![]() 两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以
两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以![]() 秒计算,声音在空气中的传播速度为
秒计算,声音在空气中的传播速度为![]() ).
).
【答案】(1)![]() 、
、![]() 两点分别在圆弧的中点,最远距离为
两点分别在圆弧的中点,最远距离为![]()
![]() ;
;
(2)音响距中轴线距离约为![]() 时为最佳放置点;
时为最佳放置点;
【解析】
(1)分别取两半圆的圆心为![]() 。根据题意
。根据题意![]() ,利用三角形的性质可证出.
,利用三角形的性质可证出.
(2)以![]() 所在的直线为
所在的直线为![]() 轴, 以中轴线
轴, 以中轴线![]() 为
为![]() 轴建立平面直角坐标系,求出
轴建立平面直角坐标系,求出![]() ,
,
利用双曲线的定义可得![]() ,设双曲线方程为
,设双曲线方程为![]() ,将点
,将点![]() 代入方程,从而求出
代入方程,从而求出![]() ,进而求出
,进而求出![]() 即可求解.
即可求解.
(1)分别取两半圆的圆心为![]()
由题意可得![]()
当![]() 四点共线时,
四点共线时,![]() 、
、![]() 两点间的距离最大,
两点间的距离最大,
此时![]() 、
、![]() 两点分别在圆弧的中点,距离为
两点分别在圆弧的中点,距离为![]()
![]()
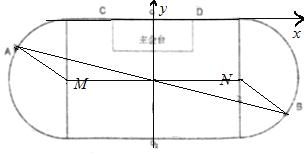
(2)以![]() 所在的直线为
所在的直线为![]() 轴, 以中轴线
轴, 以中轴线![]() 为
为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,
则 ![]() ,
,![]()
根据题意可得![]() ,
,
![]() 、
、![]() 两点在以
两点在以![]() 为焦点的双曲线上,
为焦点的双曲线上, ![]() ,即
,即![]() ,
,
设双曲线方程为:![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即音响距中轴线距离约为![]() 时为最佳放置点.
时为最佳放置点.


科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:

(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取2人,求至少有一人考核优秀的概率;
的学生中任取2人,求至少有一人考核优秀的概率;
(Ⅲ)记![]() 表示学生的考核成绩在区间
表示学生的考核成绩在区间![]() 的概率,根据以往培训数据,规定当
的概率,根据以往培训数据,规定当![]() 时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别为
轴上,短轴长分别为![]() ,
,![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为![]() ,记
,记![]() ,
,![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() .
.
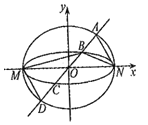
(1)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线![]() ,使得
,使得![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com