
【题目】已知首项为![]() 的等比数列
的等比数列![]() 不是递减数列,其前n项和为
不是递减数列,其前n项和为![]() ,且
,且![]() 成等差数列。
成等差数列。
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的最大项的值与最小项的值。
的最大项的值与最小项的值。
【答案】(1)![]() ;(2)最大项的值为
;(2)最大项的值为![]() ,最小项的值为
,最小项的值为![]()
【解析】
试题
(1)根据![]() 成等差数列,利用等比数列通项公式和前
成等差数列,利用等比数列通项公式和前![]() 项和公式,展开.利用等比数列
项和公式,展开.利用等比数列![]() 不是递减数列,可得
不是递减数列,可得![]() 值,进而求通项.
值,进而求通项.
(2)首先根据(1)得到![]() ,进而得到
,进而得到![]() ,但是等比数列的公比是负数,所以分两种情况:当的当n为奇数时,
,但是等比数列的公比是负数,所以分两种情况:当的当n为奇数时,![]() 随n的增大而减小,所以
随n的增大而减小,所以![]() ;当n为偶数时,
;当n为偶数时,![]() 随n的增大而增大,所以
随n的增大而增大,所以![]() ,然后可判断最值.
,然后可判断最值.
试题解析:
(1)设![]() 的公比为q。由
的公比为q。由![]() 成等差数列,得
成等差数列,得
![]() .
.
即![]() ,则
,则![]() .
.
又![]() 不是递减数列且
不是递减数列且![]() ,所以
,所以![]() .
.
故![]() .
.
(2)由(1)利用等比数列的前![]() 项和公式,可得得
项和公式,可得得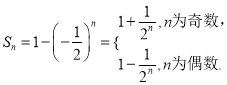
当n为奇数时,![]() 随n的增大而减小,所以
随n的增大而减小,所以![]() ,
,
故![]() .
.
当n为偶数时,![]() 随n的增大而增大,所以
随n的增大而增大,所以![]() ,
,
故![]() .
.
综上,对于![]() ,总有
,总有![]() ,
,
所以数列![]() 最大项的值为
最大项的值为![]() ,最小值的值为
,最小值的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】改革开放![]() 年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各
年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各![]() 人,进行问卷测评,所得分数的频率分布直方图如图所示在
人,进行问卷测评,所得分数的频率分布直方图如图所示在![]() 分以上为交通安全意识强.
分以上为交通安全意识强.

![]() 求
求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
![]() 已知交通安全意识强的样本中男女比例为
已知交通安全意识强的样本中男女比例为![]() ,完成下列
,完成下列![]() 列联表,并判断有多大把握认为交通安全意识与性别有关;
列联表,并判断有多大把握认为交通安全意识与性别有关;
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
![]() 用分层抽样的方式从得分在
用分层抽样的方式从得分在![]() 分以下的样本中抽取
分以下的样本中抽取![]() 人,再从
人,再从![]() 人中随机选取
人中随机选取![]() 人对未来一年内的交通违章情况进行跟踪调查,求至少有
人对未来一年内的交通违章情况进行跟踪调查,求至少有![]() 人得分低于
人得分低于![]() 分的概率.
分的概率.
附: 其中
其中![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2019年,石室2160岁!文翁兴学2160周年纪念活动于2019年11月9日在石室中学文庙校区运动场隆重召开,会场是由一个长![]() ,宽
,宽![]() 的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线
的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线![]() 对称,图形如下.
对称,图形如下.
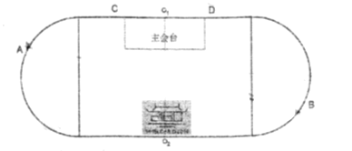
(1)若![]() 、
、![]() 两位同学分别在左右两个半圆弧上值勤,则
两位同学分别在左右两个半圆弧上值勤,则![]() 、
、![]() 两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
(2)在(1)问的情况下,若要在主会台后的会场边界上关于中轴线对称的两点![]() 、
、![]() 处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时
处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时![]() 、
、![]() 两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以
两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以![]() 秒计算,声音在空气中的传播速度为
秒计算,声音在空气中的传播速度为![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月17日是我国第6个“扶贫日”,某医院开展扶贫日“送医下乡”医疗义诊活动,现有五名医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院![]() ,医生乙只能分配到医院
,医生乙只能分配到医院![]() 或医院
或医院![]() ,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )
,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有( )
A.18种B.20种C.22种D.24种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com