
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
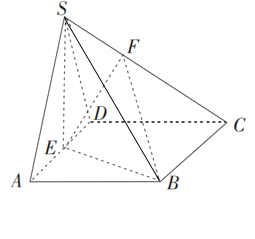
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织了一次新高考质量测评,在成绩统计分析中,某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:

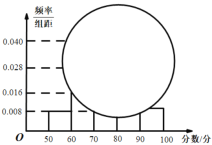
(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定90分及其以上为优秀,现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况,求在抽取的2份试卷中至少有1份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
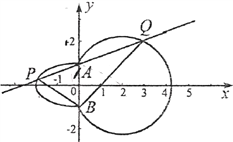
【题目】如图,曲线![]() 由左半椭圆
由左半椭圆![]() 和圆
和圆![]() 在
在![]() 轴右侧的部分连接而成,
轴右侧的部分连接而成, ![]() ,
, ![]() 是
是![]() 与
与![]() 的公共点,点
的公共点,点![]() ,
, ![]() (均异于点
(均异于点![]() ,
, ![]() )分别是
)分别是![]() ,
, ![]() 上的动点.
上的动点.
(Ⅰ)若![]() 的最大值为
的最大值为![]() ,求半椭圆
,求半椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且
,且![]() ,
, ![]() ,求半椭圆
,求半椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.
(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;
(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,
,![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.
![]() 求直线PB与平面POC所成角的余弦值.
求直线PB与平面POC所成角的余弦值.
![]() 求B点到平面PCD的距离.
求B点到平面PCD的距离.
![]() 线段PD上是否存在一点Q,使得二面角
线段PD上是否存在一点Q,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数![]() 的一条对称轴是
的一条对称轴是![]() ;
;
②函数![]() 的图象关于点(
的图象关于点(![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④若![]() ,则
,则![]() ,其中
,其中![]()
以上四个命题中正确的有 (填写正确命题前面的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com