
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 且
且![]()
![]() 上最小值为
上最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据奇函数定义确定![]() ,代入可得实数
,代入可得实数![]() 的值,再利用定义证明
的值,再利用定义证明![]() 时,函数为奇函数,(2)先研究函数单调性:为
时,函数为奇函数,(2)先研究函数单调性:为![]() 上的单调递增函数,再利用奇函数和单调性转化不等式
上的单调递增函数,再利用奇函数和单调性转化不等式
![]() ,最后再根据一元二次不等式恒成立,利用判别式恒负求实数
,最后再根据一元二次不等式恒成立,利用判别式恒负求实数![]() 的取值范围;(3)先根据条件
的取值范围;(3)先根据条件![]() ,解出
,解出![]() 的值.再根据
的值.再根据![]() 与
与![]() 的关系,将函数
的关系,将函数![]() 转化为一元二次函数,根据对称轴与定义区间位置关系讨论最小值取法,最后由最小值为
转化为一元二次函数,根据对称轴与定义区间位置关系讨论最小值取法,最后由最小值为![]() ,求出
,求出![]() 的值.
的值.
试题解析:解:(1)因为![]() 是定义域为
是定义域为![]() 的奇函数,所以
的奇函数,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
(2)由(1)知:![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() 且
且![]() ,所以
,所以![]() ,
,
所以![]() 是
是![]() 上的单调递增,
上的单调递增,
又![]() 是定义域为
是定义域为![]() 的奇函数,
的奇函数,
所以![]()
即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,即
,即![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,所以
,所以![]() ,
,
因为![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
因为![]() 的对称轴为
的对称轴为![]()
所以当![]() 时,
时, ![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
当![]() 时,
时, ![]() ,解得
,解得![]() ,
,
综上可知:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 与圆
与圆![]() 在第一象限的公共点,其中圆心
在第一象限的公共点,其中圆心![]() ,点
,点![]() 到
到![]() 的焦点
的焦点![]() 的距离与
的距离与![]() 的半径相等,
的半径相等, ![]() 上一动点到其准线与到点
上一动点到其准线与到点![]() 的距离之和的最小值等于
的距离之和的最小值等于![]() 的直径,
的直径, ![]() 为坐标原点,则直线
为坐标原点,则直线![]() 被圆
被圆![]() 所截得的弦长为( )
所截得的弦长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
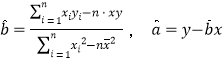 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是定义在R上的二次函数f(x)的部分图像,图2是函数![]() 的部分图像。
的部分图像。

(Ⅰ) 分别求出函数![]() 和
和![]() 的解析式;
的解析式;
(Ⅱ)如果函数![]() 在区间
在区间![]() 上是单调递减函数,求
上是单调递减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?


(Ⅱ)将上述调查所得到的频率视为概率. 现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为![]() . 若每次抽取的结果是相互独立的,求
. 若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:临界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
随机量变

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com