
【题目】已知函数![]() ,
,![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)讨论f(x)的单调性;
(2)函数g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国境内一座连接中国香港、广东珠海和中国澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术闻名世界,为内地前往香港的游客提供了便捷的交通途径,某旅行社分年龄统计了大桥落地以后,由香港大桥实现内地前往香港的老中青旅客的比例分别为![]() ,现使用分层抽样的方法从这些旅客中随机抽取
,现使用分层抽样的方法从这些旅客中随机抽取![]() 名,若青年旅客抽到60人,则( )
名,若青年旅客抽到60人,则( )

A.老年旅客抽到150人B.中年旅客抽到20人
C.![]() D.被抽到的老年旅客以及中年旅客人数之和超过200
D.被抽到的老年旅客以及中年旅客人数之和超过200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个数列![]() ,在这个数列里,任取
,在这个数列里,任取![]() 项,并且不改变它们在数列
项,并且不改变它们在数列![]() 中的先后次序,得到的数列称为数列
中的先后次序,得到的数列称为数列![]() 的一个
的一个![]() 阶子数列.
阶子数列.
已知数列![]() 的通项公式为
的通项公式为![]() (
(![]() 为常数),等差数列
为常数),等差数列![]() 是
是
数列![]() 的一个3阶子数列.
的一个3阶子数列.
(1)求![]() 的值;
的值;
(2)等差数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,且
阶子数列,且
![]() (
(![]() 为常数,
为常数,![]() ,求证:
,求证:![]() ;
;
(3)等比数列![]() 是
是![]() 的一个
的一个![]() 阶子数列,
阶子数列,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放![]() 年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各
年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各![]() 人,进行问卷测评,所得分数的频率分布直方图如图所示在
人,进行问卷测评,所得分数的频率分布直方图如图所示在![]() 分以上为交通安全意识强.
分以上为交通安全意识强.

![]() 求
求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
![]() 已知交通安全意识强的样本中男女比例为
已知交通安全意识强的样本中男女比例为![]() ,完成下列
,完成下列![]() 列联表,并判断有多大把握认为交通安全意识与性别有关;
列联表,并判断有多大把握认为交通安全意识与性别有关;
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
![]() 用分层抽样的方式从得分在
用分层抽样的方式从得分在![]() 分以下的样本中抽取
分以下的样本中抽取![]() 人,再从
人,再从![]() 人中随机选取
人中随机选取![]() 人对未来一年内的交通违章情况进行跟踪调查,求至少有
人对未来一年内的交通违章情况进行跟踪调查,求至少有![]() 人得分低于
人得分低于![]() 分的概率.
分的概率.
附: 其中
其中![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元2019年,石室2160岁!文翁兴学2160周年纪念活动于2019年11月9日在石室中学文庙校区运动场隆重召开,会场是由一个长![]() ,宽
,宽![]() 的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线
的长方形及两个以长方形宽为直径的半圆相接组成,整个会场关于中轴线![]() 对称,图形如下.
对称,图形如下.
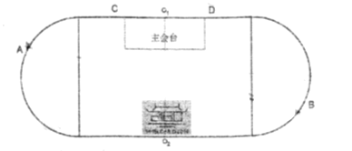
(1)若![]() 、
、![]() 两位同学分别在左右两个半圆弧上值勤,则
两位同学分别在左右两个半圆弧上值勤,则![]() 、
、![]() 两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
两位同学在圆弧什么位置时相距最远,距离为多少?并说明原因.
(2)在(1)问的情况下,若要在主会台后的会场边界上关于中轴线对称的两点![]() 、
、![]() 处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时
处分别放置两个音响,为了达到最好听觉效果,两个音响的距离要足够大,同时![]() 、
、![]() 两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以
两位同学听到两个音响传来的声音时间差不超过0.18秒,求音响距中轴线距离约为多少时为最佳放置点.(注:不超过0.18秒以![]() 秒计算,声音在空气中的传播速度为
秒计算,声音在空气中的传播速度为![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com