
【题目】已知函数f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)讨论f(x)的单调性;
(2)函数g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
【答案】(1) 当a>6时,f(x)在(![]() ,+∞),(0,2)上单调递增,在(2,
,+∞),(0,2)上单调递增,在(2,![]() )上单调递减.
)上单调递减.
当a=6时,f(x)在(0,+∞)上单调递增.
当0<a<6时,f(x)在(2,+∞),(0,![]() )上单调递增,f(x)在(
)上单调递增,f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
当a≤0时,f(x)在(2,+∞)上单调递增.
(2) (﹣5,+∞).
【解析】
(1)首先对f(x)求导数,令![]() ,再讨论当
,再讨论当![]() 、a=6、
、a=6、![]() 、
、![]() 四种情况对应的单调性。
四种情况对应的单调性。
(2)首先由f(x)<g(x),化简得4lnx+1<(6+a)x,因为x∈[1,e],所以a>[![]() ]min,
]min,
令h(x)![]() ,对 h(x)求导判断其单调性即可。求出最小值即可。
,对 h(x)求导判断其单调性即可。求出最小值即可。
(1)f′(x)=3x﹣(6+a)![]() (x>0),
(x>0),
令f′(x)=0,得x1![]() ,x2=2,
,x2=2,
①当![]() 及a>6时,
及a>6时,
若x∈(![]() ,+∞)∪(0,2),f′(x)>0,故f(x)在(
,+∞)∪(0,2),f′(x)>0,故f(x)在(![]() ,+∞),(0,2)上单调递增,
,+∞),(0,2)上单调递增,
若x∈(2,![]() ),f′(x)<0,故f(x)在(2,
),f′(x)<0,故f(x)在(2,![]() )上单调递减.
)上单调递减.
②当a=6时,f′(x)≥0对x∈(0,+∞)恒成立,
故f(x)在(0,+∞)上单调递增.
③当0![]() 2,即0<a<6时,
2,即0<a<6时,
若x∈(2,+∞)∪(0,![]() ),f′(x)>0,故f(x)在(2,+∞),(0,
),f′(x)>0,故f(x)在(2,+∞),(0,![]() )上单调递增
)上单调递增
若x∈(![]() ,2),f′(x)<0,故f(x)在(
,2),f′(x)<0,故f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
④当![]() ,即a≤0时,
,即a≤0时,
若x∈(2,+∞),f′(x)>0,故f(x)在(2,+∞)上单调递增,
若x∈(0,2),f′(x)<0,f(x)在(0,2)单调递减.
综上所述:当a>6时,f(x)在(![]() ,+∞),(0,2)上单调递增,在(2,
,+∞),(0,2)上单调递增,在(2,![]() )上单调递减.
)上单调递减.
当a=6时,f(x)在(0,+∞)上单调递增.
当0<a<6时,f(x)在(2,+∞),(0,![]() )上单调递增,f(x)在(
)上单调递增,f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
当a≤0时,f(x)在(2,+∞)上单调递增.
(2)当x∈[1,e],由f(x)<g(x),化简得4lnx+1<(6+a)x,
因为x∈[1,e],所以a>[![]() ]min,
]min,
令h(x)![]() ,
,![]() ,
,
令h′(x)=0,得x=e![]() ,
,
当x∈[1,e![]() )时,h′(x)>0,h(x)单调递增.
)时,h′(x)>0,h(x)单调递增.
当x∈(e![]() ,e]时,h′(x)<0,h(x)单调递减.
,e]时,h′(x)<0,h(x)单调递减.
所以h(x)min={h(1),h(e)},
h(1)=﹣5<h(e)![]() ,
,
所以a>﹣5,
故a的取值范围是(﹣5,+∞).


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
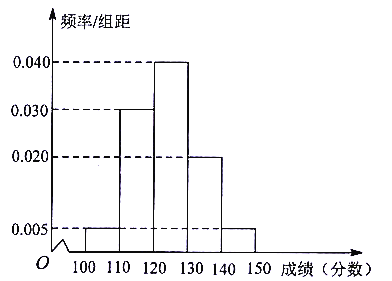
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是民航部门统计的某年春运期间,六个城市售出的往返机票的平均价格(单位元),以及相比于上一年同期价格变化幅度的数据统计图,以下叙述不正确的是( )
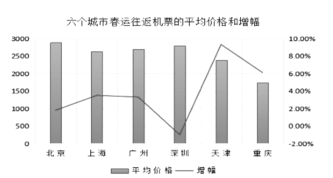
A.深圳的变化幅度最小,北京的平均价格最高
B.天津的往返机票平均价格变化最大
C.上海和广州的往返机票平均价格基本相当
D.相比于上一年同期,其中四个城市的往返机票平均价格在增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com