练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法中错误的个数是（ ）

    ①从某社区65户高收入家庭，280户中等收入家庭，105户低收入家庭中选出100户调查社会购买力的某一项指标，应采用的最佳抽样方法是分层抽样

    ②线性回归直线一定过样本中心点

    ③对于一组数据，如果将它们改变为，则平均数与方差均发生变化

    ④若一组数据1、、2、3的众数是2，则这组数据的中位数是2

    ⑤用系统抽样方法从编号为1，2，3，…，700的学生中抽样50人，若第2段中编号为20的学生被抽中，按照等间隔抽取的方法，则第5段中被抽中的学生编号为76

    A.0B.1C.2D.3

    【答案】C

    【解析】

    ①应该采用分层抽样满足抽样合理性；②线性回归直线一定过样本中心点；③平均数肯定变化，方差指数据和平均数的离散程度，不变；④由众数算出即可求中位数；⑤用系统抽样，700个抽样50每隔14人抽一次，根据第二次抽中编号为20可推知第五次被抽中的编号。

    ①从某社区65户高收入家庭，280户中等收入家庭，105户低收入家庭中选出100户调查社会购买力的某一项指标，采用分层抽样满足抽样合理性，正确；

    ②线性回归直线一定过样本中心点，正确；

    ③对于一组数据，如果将它们改变为，平均数由变为，

    方差

    没发生变，不正确；

    ④因为众数是2，所以，所以这组数据的中位数是，正确；

    ⑤用系统抽样，700个抽样50每隔14人抽一次，第二次抽中编号为20，则第三次是34，

    第四次是48.第五次是62，不正确；

    所以错误的是③⑤

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若不等式在(0，+∞)上恒成立，则a的取值范围是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆和点.

    （1）过点向圆引切线，求切线的方程；

    （2）求以点为圆心，且被直线截得的弦长为8的圆的方程；

    （3）设为（2）中圆上任意一点，过点向圆引切线，切点为，试探究：平面内是否存在一定点，使得为定值？若存在，请求出定点的坐标，并指出相应的定值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆x2＋y2－2y－1＝0关于直线y＝x对称的圆的方程是 (　　)

    A. (x－1)2＋y2＝2 B. (x＋1)2＋y2＝2 C. (x－1)2＋y2＝4 D. (x＋1)2＋y2＝4

    【答案】A

    【解析】圆 的标准方程为，所以圆心为（0,1），半径为，圆心关于直线的对称点是（1,0），所以圆x2＋y2－2y－1＝0关于直线y＝x对称的圆的方程是，选A.

    点睛：本题主要考查圆关于直线的对称的圆的方程，属于基础题。解答本题的关键是求出圆心关于直线的对称点，两圆半径相同。

    【题型】单选题
    【结束】
    8

    【题目】已知双曲线的离心率为，焦点是， ，则双曲线方程为 （ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数在上的最小值的表达式；

    （2）若函数在上有且只有一个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某个调查小组在对人们的休闲方式的一次调查中，共调查了150人，其中男性45人，女性55人。女性中有35人主要的休闲方式是室内活动，另外20人主要的休闲方式是室外运动；男性中15人主要的休闲方式是室内活动，另外30人主要的休闲方式是室外运动。

    参考数据：

    0.05

    0.025

    0.010

    0.005

    0.001

    3.841

    5.024

    6.635

    7.879

    10.828

    （1）根据以上数据建立一个的列联表；

    （2）能否在犯错误的概率不超过0.005的前提下认为休闲方式与性别有关？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”，彰显出中国式创新的强劲活力，某移动支付公司在我市随机抽取了100名移动支付用户进行调查，得到如下数据：

    每周移动支付次数

    1次

    2次

    3次

    4次

    5次

    6次及以上

    男

    4

    3

    3

    7

    8

    30

    女

    6

    5

    4

    4

    6

    20

    合计

    10

    8

    7

    11

    14

    50

    (1)在每周使用移动支付超过3次的样本中，按性别用分层抽样的方法随机抽取5名用户.

    ①求抽取的5名用户中男、女用户各多少人；

    ②从这5名用户中随机抽取2名用户，求抽取的2名用户中既有男用户又有女用户的概率.

    (2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”，能否在犯错误概率不超过的前提下，认为“喜欢使用移动支付”与性别有关？

    附表及公式：

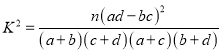
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，椭圆关于坐标轴对称，以坐标原点为极点，以轴的正半轴为极轴建立极坐标系， ， 为椭圆上两点.

    (1)求直线的直角坐标方程与椭圆的参数方程；

    (2)若点在椭圆上，且点在第一象限内，求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是定义在R上的函数,对任意的,恒有，且当时, .

    (1)求的值;

    (2)求证:对任意,恒有.

    (3)求证:在R上是减函数.

    查看答案和解析>>

    同步练习册答案