
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的最小值
上的最小值![]() 的表达式;
的表达式;
(2)若函数![]() 在
在![]() 上有且只有一个零点,求
上有且只有一个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)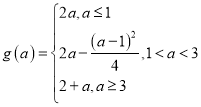 ;(2)
;(2)![]() .
.
【解析】
(1)求出函数![]() 的对称轴方程,对实数
的对称轴方程,对实数![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,分析函数
三种情况讨论,分析函数![]() 在区间
在区间![]() 上的单调性,进而可得出函数
上的单调性,进而可得出函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() 的表达式;
的表达式;
(2)对函数![]() 分情况讨论:(i)方程
分情况讨论:(i)方程![]() 在区间
在区间![]() 上有两个相等的实根;(ii)①方程
上有两个相等的实根;(ii)①方程![]() 在区间
在区间![]() 只有一根;(②
只有一根;(②![]() ;③
;③![]() .可得出关于实数
.可得出关于实数![]() 的等式或不等式,即可解得实数
的等式或不等式,即可解得实数![]() 的取值范围.
的取值范围.
(1)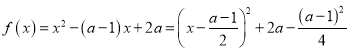 ,其对称轴为
,其对称轴为![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,![]() ;
;
当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
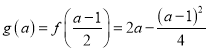 ;
;
当![]() 时,即当
时,即当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() .
.
综上所述: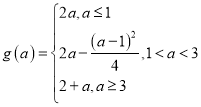 ;
;
(2)(i)若方程![]() 在
在![]() 上有两个相等的实数根,
上有两个相等的实数根,
则 ,此时无解;
,此时无解;
(ii)若方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
①当只有一根在![]() 内时,
内时,![]() ,即
,即![]() ,得
,得![]() ;
;
②当![]() 时,
时,![]() ,方程化为
,方程化为![]() ,其根为
,其根为![]() ,
,![]() ,满足题意;
,满足题意;
③当![]() 时,
时,![]() ,方程化为
,方程化为![]() ,其根为
,其根为![]() ,
,![]() ,满足题意.
,满足题意.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】某种产品的质量以其“无故障使用时间![]() (单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
(单位:小时)”衡量,无故障使用时间越大表明产品质量越好,且无故障使用时间大于3小时的产品为优质品,从某企业生产的这种产品中抽取100件,并记录了每件产品的无故障使用时间,得到下面试验结果:
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品,求至少有一件是优质品的概率;
(2)若该企业生产的这种产品每件销售利润![]() (单位:元)与其无故障使用时间
(单位:元)与其无故障使用时间![]() 的关系式为
的关系式为
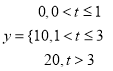
从该企业任取两件这种产品,其利润记为![]() (单位:元),求
(单位:元),求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国第一高摩天轮“南昌之星摩天轮”高度为![]() ,其中心
,其中心![]() 距地面
距地面![]() ,半径为
,半径为![]() ,若某人从最低点
,若某人从最低点![]() 处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间
处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间![]() 变化,
变化,![]() 后达到最高点,从登上摩天轮时开始计时.
后达到最高点,从登上摩天轮时开始计时.
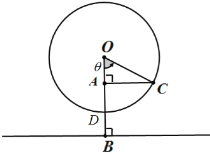
(1)求出人与地面距离![]() 与时间
与时间![]() 的函数解析式;
的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是分层抽样
②线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
③对于一组数据![]() ,如果将它们改变为
,如果将它们改变为![]() ,则平均数与方差均发生变化
,则平均数与方差均发生变化
④若一组数据1、![]() 、2、3的众数是2,则这组数据的中位数是2
、2、3的众数是2,则这组数据的中位数是2
⑤用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,按照等间隔抽取的方法,则第5段中被抽中的学生编号为76
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=![]() ,AD=2,PA=PD=
,AD=2,PA=PD=![]() ,E,F分别是棱AD,PC的中点.
,E,F分别是棱AD,PC的中点.

(1)证明:EF∥平面PAB;
(2)若二面角P-AD-B为60°.
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com