
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)![]() 的定义域为
的定义域为![]() ,求导可得
,求导可得![]() .则考查函数的单调性只需考查二次函数
.则考查函数的单调性只需考查二次函数![]() 的性质可得:
的性质可得:
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减.
上单调递减.
(2)原问题等价于![]() ,
, ![]() 恒成立. 构造函数,令
恒成立. 构造函数,令![]() ,则
,则![]() ,
, ![]() ,即
,即![]() 在
在![]() 时取得最大值.
时取得最大值.
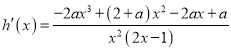 .由
.由![]() 解得
解得![]() .经检验可得a=1符合题意.故
.经检验可得a=1符合题意.故![]() .
.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, ![]() .
.
∵![]() .
.
令![]() ,则
,则
(a)若![]() ,即当
,即当![]() 时,对任意
时,对任意![]() ,
, ![]() 恒成立, 即当
恒成立, 即当![]() 时,
时, ![]() 恒成立(仅在孤立点处等号成立).
恒成立(仅在孤立点处等号成立).
∴![]() 在
在![]() 上单调递增.
上单调递增.
(b)若![]() ,即当
,即当![]() 或
或![]() 时,
时, ![]() 的对称轴为
的对称轴为![]() .
.
①当![]() 时,
时, ![]() ,且
,且![]() .
.
如图,任意![]() ,
, ![]() 恒成立, 即任意
恒成立, 即任意![]() 时,
时, ![]() 恒成立,
恒成立,
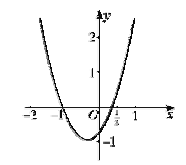
∴![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,
时, ![]() ,且
,且![]() .
.
如图,记![]() 的两根为
的两根为![]()
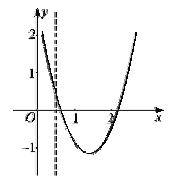
∴当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
∴当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减.
上单调递减.
(2)![]() 恒成立等价于
恒成立等价于![]() ,
, ![]() 恒成立.
恒成立.
令![]() ,则
,则![]() 恒成立等价于
恒成立等价于![]() ,
, ![]()
![]() .
.
要满足![]() 式,即
式,即![]() 在
在![]() 时取得最大值.
时取得最大值.
∵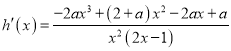 .
.
由![]() 解得
解得![]() .
.
当![]() 时,
时, 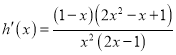 ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,从而
上单调递减,从而![]() ,符合题意.
,符合题意.
所以, ![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() 和
和![]() 均为等边三角形,且平面
均为等边三角形,且平面![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
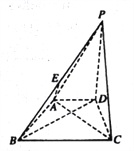
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图所示.
的一段图象如图所示.
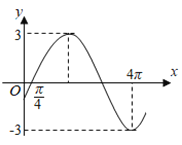
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调减区间,并指出
的单调减区间,并指出![]() 的最大值及取到最大值时
的最大值及取到最大值时![]() 的集合;
的集合;
(3)把![]() 的图象向右至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
的图象向右至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
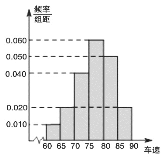
(1)调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(3)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其它两观测点晚4![]() .已知各观测点到该中心的距离是1020
.已知各观测点到该中心的距离是1020![]() .则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340
.则该巨响发生在接报中心的( )处.(假定当时声音传播的速度为340![]() ,相关各点均在同一平面上)
,相关各点均在同一平面上)
A. 西偏北![]() 方向,距离
方向,距离![]() B. 东偏南
B. 东偏南![]() 方向,距离
方向,距离![]()
C. 西偏北![]() 方向,距离
方向,距离![]() D. 东偏南
D. 东偏南![]() 方向,距离
方向,距离![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com