
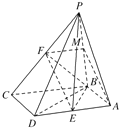
【题目】如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=![]() ,AD=2,PA=PD=
,AD=2,PA=PD=![]() ,E,F分别是棱AD,PC的中点.
,E,F分别是棱AD,PC的中点.

(1)证明:EF∥平面PAB;
(2)若二面角P-AD-B为60°.
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
试题分析:(1)要证明![]() 平面
平面![]() ,可以先证明平面
,可以先证明平面![]()
![]() ,利用线面平行的判定定理,即可证明
,利用线面平行的判定定理,即可证明![]() 平面
平面![]() ;(2)①要证明平面
;(2)①要证明平面![]() 平面
平面![]() ,可用面面垂直的判定定理,即只需证明
,可用面面垂直的判定定理,即只需证明![]() 平面
平面![]() 即可;②由①
即可;②由①![]() 平面
平面![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,由
所成的角,由![]() 及已知,得
及已知,得![]() 为直角,即可计算
为直角,即可计算![]() 的长度,在
的长度,在![]() 中,即计算直线
中,即计算直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
试题解析:(1)证明:如图,取PB中点M,连接MF,AM.
因为F为PC中点,故MF∥BC且MF=![]() BC.由已知有BC∥AD,BC=AD.
BC.由已知有BC∥AD,BC=AD.
又由于E为AD中点,因而MF∥AE且MF=AE,故四边形AMFE为平行四边形,
所以EF∥AM.又AM平面PAB,而EF平面PAB,所以EF∥平面PAB.
(2)①证明:如图,连接PE,BE.
因为PA=PD,BA=BD,而E为AD中点,故PE⊥AD,BE⊥AD,
所以∠PEB为二面角P-AD-B的平面角.
在△PAD中,由PA=PD=![]() ,AD=2,可解得PE=2.
,AD=2,可解得PE=2.
在△ABD中,由BA=BD=![]() ,AD=2,可解得BE=1.
,AD=2,可解得BE=1.
在△PEB中,PE=2,BE=1,∠PEB=60°,由余弦定理,可解得PB=![]() ,
,
从而∠PBE=90°,即BE⊥PB.
又BC∥AD,BE⊥AD,从而BE⊥BC,因此BE⊥平面PBC.
又BE平面ABCD,所以平面PBC⊥平面ABCD.
②连接BF.由①知,BE⊥平面PBC,所以∠EFB为直线EF与平面PBC所成的角.
由PB=![]() 及已知,得∠ABP为直角.
及已知,得∠ABP为直角.
而MB=![]() PB=
PB=![]() ,可得AM=
,可得AM=![]() ,故EF=
,故EF=![]() .
.
又BE=1,故在Rt△EBF中,sin∠EFB=![]() =
=![]() .
.
所以直线EF与平面PBC所成角的正弦值为![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是P(单位:万元)和Q(单位:万元),它们与投入资金t(单位:万元)的关系有经验公式P= ![]() t,Q=
t,Q= ![]() .今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(单位:万元),
.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(单位:万元),
(1)试建立总利润y(单位:万元)关于x的函数关系式;
(2)当对甲种商品投资x(单位:万元)为多少时?总利润y(单位:万元)值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() >0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
>0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
(1)求(RA)∩B;
(2)若B∪C=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
)x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表:

(I)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(II)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() 有相同的极值点.
有相同的极值点.
(I)求函数![]() 的解析式;
的解析式;
(II)证明:不等式![]() (其中e为自然对数的底数);
(其中e为自然对数的底数);
(III)不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
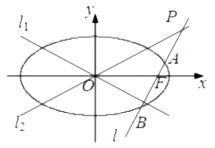
【题目】已知椭圆![]() 方程为
方程为![]() ,双曲线
,双曲线![]() 的两条渐近线分别为
的两条渐近线分别为![]() ,
, ![]() ,过椭圆
,过椭圆![]() 的右焦点作直线
的右焦点作直线![]() ,使
,使![]() ,又
,又![]() 与
与![]() 交于点
交于点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 的两个交点由上至下依次为
的两个交点由上至下依次为![]() ,
, ![]() .
.
(1)若![]() 与
与![]() 所成的锐角为
所成的锐角为![]() ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆![]() 的方程;
的方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com