
分析 (1)设切线l的方程为x=λy+6,由点到直线的距离公式得$\frac{|3-2λk-6|}{{\sqrt{1+{λ^2}}}}=3$,解得λ=$\frac{12}{5}$或λ=0,即可求过点P且与圆C相切的直线方程l;
(2)设圆心M(6,b),则半径r=|b|,要使圆M与圆C外切,则须有:|MC|=3+|b|,求出b,即可求圆M的方程.
解答 (1)解:圆C化为标准方程是(x-3)2+(y-2)2=9…(1分)
故圆心坐标为C(3,2)半径r=3.
设切线l的方程为x=λy+6…(2分)
即x-λy-6=0,由点到直线的距离公式得$\frac{|3-2λk-6|}{{\sqrt{1+{λ^2}}}}=3$,解得λ=$\frac{12}{5}$或λ=0.
所以切线l的方程为 5x-12y-30=0或x=6…(5分)
(2)设圆心M(6,b),则半径r=|b|
∴要使圆M与圆C外切,则须有:|MC|=3+|b|…(8分)
∴$\sqrt{{{(6-3)}^2}+{{(b-2)}^2}}=|b|+3$化简得4b+6|b|=4解得$b=\frac{2}{5}$或b=-2
所以圆M的方程为${(x-6)^2}+{(y-\frac{2}{5})^2}=\frac{4}{25}$或(x-6)2+(y+2)2=4.…(10分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查点到直线距离公式的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
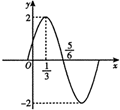 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则要得到y=f(x)的图象,只需要把y=Asinωx的图象( )
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则要得到y=f(x)的图象,只需要把y=Asinωx的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{1}{6}$个单位 | D. | 向右平移$\frac{1}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,+∞) | B. | [-2,2] | C. | (-∞,-2] | D. | [-$\frac{5}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com