练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料的主要原料是磷酸盐4吨，硝酸盐18吨；生产1车皮乙种肥料需要的主要原料是磷酸盐1吨，硝酸盐15吨．现库存磷酸盐10吨，硝酸盐66吨，在此基础上生产这两种混合肥料．如果生产1车皮甲种肥料产生的利润为12 000元，生产1车皮乙种肥料产生的利润为7 000元，那么可产生的最大利润是（ ）
    A.29 000元
    B.31 000元
    C.38 000元
    D.45 000元

    【答案】C
    【解析】解：设x、y分别表示计划生产甲、乙两种肥料的车皮数． 由题意，得 ．
    工厂的总利润z=12000x+7000y
    由约束条件得可行域如图，
    由 ，解得： ，
    所以最优解为A（2，2），
    则当直线12000x+7000y﹣z=0过点A（2，2）时，
    z取得最大值为：38000元，即生产甲、乙两种肥料各2车皮时可获得最大利润．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|x﹣a|，a∈R． （Ⅰ）当a=2时，解不等式：f（x）≥6﹣|2x﹣5|；
    （Ⅱ）若关于x的不等式f（x）≤4的解集为[﹣1，7]，且两正数s和t满足2s+t=a，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=xlnx．
    （1）不等式f（x）＞kx﹣ 对于任意正实数x均成立，求实数k的取值范围；
    （2）是否存在整数m，使得对于任意正实数x，不等式f（m+x）＜f（m）ex恒成立？若存在，求出最小的整数m，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：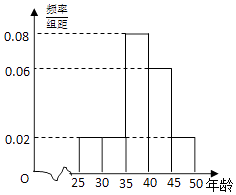
    （1）如表是年龄的频数分布表，求a，b的值；

    区间

    [25，30）

    [30，35）

    [35，40）

    [40，45）

    [45，50]

    人数

    50

    50

    a

    150

    b


    （2）根据频率分布直方图估计志愿者年龄的平均数和中位数；
    （3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
    （4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}满足，a2=3，a5=81．
    （1）求数列{an}的通项公式；
    （2）设bn=log3an ， 求{bn}的前n项和为Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某高中随机选取5名高一男生，其身高和体重的数据如表所示：

    身高x（cm）

    160

    165

    170

    175

    180

    体重y（kg）

    63

    66

    70

    72

    74

    根据如表可得回归方程 =0.56x+ ，据此模型可预报身高为172cm的高一男生的体重为（ ）
    A.70.12kg
    B.70.29kg
    C.70.55kg
    D.71.05kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn满足Sn= n2+ n（n∈N*），数列{bn}是首项为4的正项等比数列，且2b2 ， b3﹣3，b2+2成等差数列． （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）令cn=anbn（n∈N*），求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax2﹣2ax+b，当x∈[0，3]时，|f（x）|≤1恒成立，则2a+b的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图． （Ⅰ）求直方图中a的值；
    （Ⅱ）若该市有110万居民，估计全市居民中月均用水量不低于3吨的人数，请说明理由；
    （Ⅲ）若该市政府希望使80%的居民每月的用水量不超过标准x（吨），估计x的值（精确到0.01），并说明理由．

    查看答案和解析>>

    同步练习册答案