
【题目】已知数列{an}的前n项和Sn满足Sn= ![]() n2+
n2+ ![]() n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
n(n∈N*),数列{bn}是首项为4的正项等比数列,且2b2 , b3﹣3,b2+2成等差数列. (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=anbn(n∈N*),求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)∵数列{an}的前n项和Sn满足Sn= ![]() n2+
n2+ ![]() n(n∈N*),
n(n∈N*),
∴a1=S1= ![]() =5,
=5,
当n≥2时,an=Sn﹣Sn﹣1=( ![]() )﹣[
)﹣[ ![]() ]
]
=3n+2,
当n=1时,上式成立,
∴数列{an}的通项公式为an=3n+2.
∵数列{bn}是首项为4的正项等比数列,且2b2,b3﹣3,b2+2成等差数列,
∴ 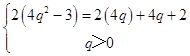 ,解得q=2.
,解得q=2.
∴数列{bn}的通项公式bn=4×2n﹣1=2n+1.
(Ⅱ)∵cn=anbn=(3n+2)2n+1=(6n+4)2n,
∴数列{cn}的前n项和:
Tn=10×2+16×22+22×23+…+(6n+4)×2n,①
2Tn=10×22+16×23+22×23+…+(6n+4)×2n+1,②
①﹣②,得:
﹣Tn=20+6(22+23+…+2n)﹣(6n+4)×2n+1
=20+6× ![]() ﹣(6n+4)×2n+1
﹣(6n+4)×2n+1
=﹣4﹣(6n﹣2)×2n+1,
∴Tn=(6n﹣2)×2n+1+4
【解析】(Ⅰ)由数列{an}的前n项和Sn满足Sn= ![]() n2+
n2+ ![]() n(n∈N*),得到a1=S1=5,当n≥2时,an=Sn﹣Sn﹣1=3n+2,由此能求出数列{an}的通项公式;由数列{bn}是首项为4的正项等比数列,且2b2,b3﹣3,b2+2成等差数列,利用等比数列通项公式、等差数列性质列出方程,求出公比,由此能求出数列{bn}的通项公式.(Ⅱ)由cn=anbn=(3n+2)2n+1=(6n+4)2n,利用错位相减法能求出数列{cn}的前n项和.
n(n∈N*),得到a1=S1=5,当n≥2时,an=Sn﹣Sn﹣1=3n+2,由此能求出数列{an}的通项公式;由数列{bn}是首项为4的正项等比数列,且2b2,b3﹣3,b2+2成等差数列,利用等比数列通项公式、等差数列性质列出方程,求出公比,由此能求出数列{bn}的通项公式.(Ⅱ)由cn=anbn=(3n+2)2n+1=(6n+4)2n,利用错位相减法能求出数列{cn}的前n项和.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系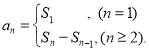 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】一组数据如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 1.3 | 1.9 | 2.5 | 2.7 | 3.6 |
(1)画出散点图;
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A.29 000元
B.31 000元
C.38 000元
D.45 000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡2(bmod4).下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( ) 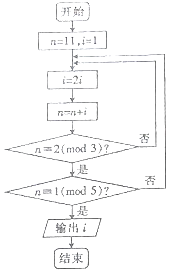
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: 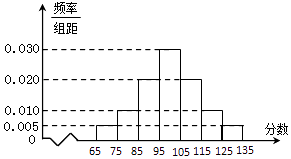
(1)求这部分学生成绩的样本平均数 ![]() 和样本方差s2(同一组数据用该组的中点值作为代表)
和样本方差s2(同一组数据用该组的中点值作为代表)
(2)由频率分布直方图可以认为,该校高二学生在这次测验中的数学成绩X服从正态分布 ![]() . ①利用正态分布,求P(X≥129);
. ①利用正态分布,求P(X≥129);
②若该校高二共有1000名学生,试利用①的结果估计这次测验中,数学成绩在129分以上(含129分)的学生人数.(结果用整数表示)
附:① ![]() ≈14.5②若X~N(μ,σ2),则P(μ﹣2σ<X<μ+2σ)=0.9544.
≈14.5②若X~N(μ,σ2),则P(μ﹣2σ<X<μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),满足f(x+1)=f(x﹣1),且f(x)在[﹣3,﹣2]上是增函数,又α、β是锐角三角形的两个内角,则( )
A.f(sinα)>f(cosβ)
B.f(cosα)<f(cosβ)
C.f(sinα)<f(cosβ)
D.f(sinα)<f(sinβ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com