
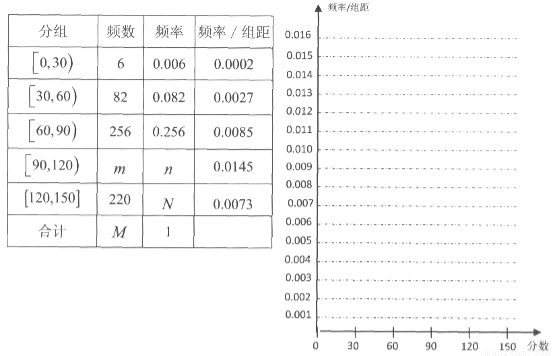
2013年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
(2)若2013年北京市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
(1)M=1000,m=436,n=0.436,N=0.220,频率分布直方图详见试题解析;
(2)全市文科数学成绩在90及90分以上的人数为13120;
(3)7人中录取2人恰有1人为女生的概率为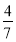 .
.
【解析】
试题分析:(1)由表格容易求出m、n、M、N的值,频率分布直方图详见试题解析;
(2)由古典概型可以求出全市文科数学成绩在90及90分以上的人数为13120;
(3)设4名男生分别表示为A1、A2、A3、A4,3名女生分别表示为B1、B2、B3,列举出从7名学生中录取2名学生的基本事件有21种,满足条件的有12种,因此7人中录取2人恰有1人为女生的概率为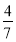 .
.
试题解析:(1)如图
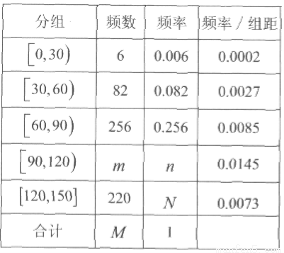
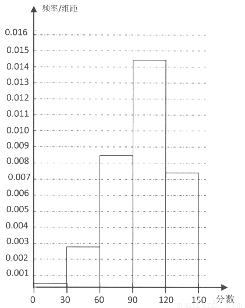
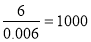 ,则M=1000,m=436,n=0.436,N=0.220. 5分
,则M=1000,m=436,n=0.436,N=0.220. 5分
(2)设全市文科数学成绩在90及90分以上的人数为x,则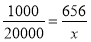 ,x=13120. 7分
,x=13120. 7分
(3)设4名男生分别表示为A1、A2、A3、A4,3名女生分别表示为B1、B2、B3则从7名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A2,B3),(A3,A4),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
(B1,B2),(B1,B3),(B2,B3),共21种.
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
共12种,
则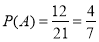 .
.
故7人中录取2人恰有1人为女生的概率为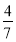 . 9分
. 9分
考点:频率分布直方图、古典概型.


科目:高中数学 来源:2015届北京海淀区高二上学期期末考试文科数学试卷(解析版) 题型:选择题
已知命题 函数
函数 是增函数,命题
是增函数,命题
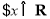 ,
, 的导数大于0,那么 ( )
的导数大于0,那么 ( )
(A) 是真命题 (B)
是真命题 (B) 是假命题
是假命题
(C) 是真命题 (D)
是真命题 (D) 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
平面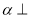 平面
平面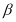 的一个充分条件是
的一个充分条件是
A. 存在一条直线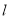 ,
,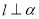 且
且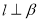
B. 存在一个平面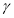 ,
,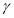 ∥
∥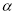 且
且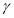 ∥
∥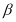
C. 存在一个平面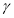 ,
,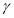 ⊥
⊥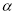 且
且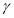 ⊥
⊥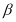
D. 存在一条直线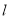 ,
,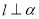 且
且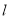 ∥
∥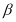
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
已知抛物线 的准线与双曲线
的准线与双曲线  交于
交于 ,
, 两点,点
两点,点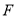 为抛物线的焦点,若△
为抛物线的焦点,若△ 为直角三角形,则
为直角三角形,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试理科数学试卷(解析版) 题型:填空题
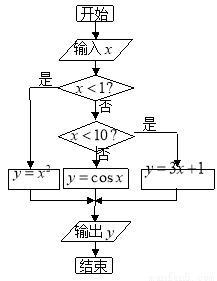
根据如图所示的程序框图,若输出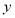 的值为4,则输入的
的值为4,则输入的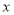 值为______________.
值为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com