分析:(1)以C为坐标原点,建立如图所示的空间坐标系,我们易求出A1B与C1M的方向向量,然后根据他们的数量积为0,易判断A1B⊥C1M;
(2)根据N为AA1的中点CA=CB=2,棱AA1=4,求出B,N两点的坐标,代入空间两点间的距离公式,即可求出BN的长;
(3)分别求出平面B1A1E与平面A1EC1的法向量,我们代入向量的夹角公式即可求出二面角B1-A1E-C1平面角的余弦值.
解答: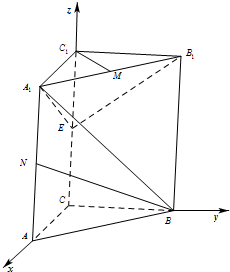
证明:(1)如图建立空间直角坐标系
A
1(2,0,4),B(0,2,0),C
1(0,0,4),M(1,1,4),
=(-2,2,-4),=(1,1,0)∴
•=-2+2=0∴A
1B⊥C
1M(4分)
(2)依题意得:B(0,2,0),N(2,0,2)
∴
|BN|==2.(6分)
(3)依题意得:A
1(2,0,4),B(0,2,0),C(0,0,0),B
1(0,2,4)E(0,0,2),C
1(0,0,4)
∴
=(0,2,2),=(2,0,2)∵BC⊥AC,BC⊥CC
1∴平面C
1EA
1的法向量为
=(0,2,0),得
||=2设平面B
1EA
1的法向量为
=(x,y,z)则:
•=0得:2y+2z=0∴y=-z•=0得:2+2z=0∴x=-z令
z=1,则=(-1,-1,1),得
||=则
cos<,>===-由题意可知:二面角B
1-A
1E-C
1的大小是锐角
所以二面角B
1-A
1E-C
1的平面角的余弦值是
..(13分)
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的性质,其中建立空间坐标系,将线线垂直,二面角问题转化为向量夹角问题是解答本题的关键.

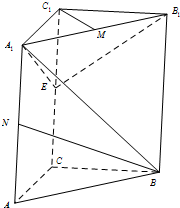 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,棱AA1=4,E、M、N分别是CC1、A1B1、AA1的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,棱AA1=4,E、M、N分别是CC1、A1B1、AA1的中点. 证明:(1)如图建立空间直角坐标系
证明:(1)如图建立空间直角坐标系

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点. 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
