练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，正三棱柱的高为2，是的中点，是的中点

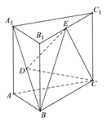
    （1）证明：平面；

    （2）若三棱锥的体积为，求该正三棱柱的底面边长.

    【答案】(1)见解析(2)2

    【解析】

    试题分析：（1）由三角形中位线性质得DE//AC1，再根据线面平行判定定理得结果（2）根据平行性质得D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半，再根据锥体体积公式列方程解得底面边长

    试题解析：（Ⅰ）证明：如图，连接AB1，AC1，

    易知D是AB1的中点，

    又E是B1C1的中点，

    所以在中，DE//AC1，

    又DE平面ACC1A1，AC1平面ACC1A1，

    所以DE//平面ACC1A1.

    （Ⅱ）解：，

    D是AB1的中点，

    D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半，

    如图，作AFBC交BC于F，由正三棱柱的性质，易证AF平面BCC1B1，

    设底面正三角形边长为，则三棱锥DEBC的高h=AF=，

    ，所以，

    解得.

    所以该正三棱柱的底面边长为2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，输出的结果为1538，则判断框内可填入的条件为（ ）

    A.n＞6？
    B.n＞7？
    C.n＞8？
    D.n＞9？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】石嘴山三中最强大脑社对高中学生的记忆力x和判断力y进行统计分析，得下表数据

    x

    6

    8

    10

    12

    y

    2

    3

    5

    6

    （1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程 ，预测记忆力为9的同学的判断力．

    （2）若记忆力增加5个单位，预测判断力增加多少个单位？

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆心在轴上的圆与直线切于点.圆： ．

    （1）求圆的标准方程；

    （2）已知，圆与轴相交于两点（点在点的右侧）．过点任作一条倾斜角不为0的直线与圆相交于两点．问：是否存在实数，使得？若存在，求出实数的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】遂宁市观音湖港口船舶停靠的方案是先到先停．

    （1）若甲乙两艘船同时到达港口，双方约定各派一名代表从1，2，3，4，5中各随机选一个数（甲、乙选取的数互不影响），若两数之和为偶数，则甲先停靠；若两数之和为奇数，则乙先停靠，这种规则是否公平？请说明理由．

    （2）根据以往经验，甲船将于早上7:00～8:00到达，乙船将于早上7:30～8:30到达，请求出甲船先停靠的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果执行右边的程序框图，输入正整数N（N≥2）和实数a1 ， a2 ， …，an ， 输出A，B，则（ ）

    A.A+B为a1 ， a2 ， …，an的和
    B. 为a1 ， a2 ， …，an的算术平均数
    C.A和B分别是a1 ， a2 ， …，an中最大的数和最小的数
    D.A和B分别是a1 ， a2 ， …，an中最小的数和最大的数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC﹣A1B1C1中，AC=BC= AA1 ， D是棱AA1的中点，DC1⊥BD

    （1）证明：DC1⊥BC；
    （2）求二面角A1﹣BD﹣C1的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）在[a，b]上有定义，若对任意x1 ， x2∈[a，b]，有 则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
    ①f（x）在[1，3]上的图象是连续不断的；
    ②f（x2）在[1， ]上具有性质P；
    ③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
    ④对任意x1 ， x2 ， x3 ， x4∈[1，3]，有 [f（x1）+f（x2）+f（x3）+f（x4）]
    其中真命题的序号是（ ）
    A.①②
    B.①③
    C.②④
    D.③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设一组数据的平均数是2.8，方差是3.6，若将这组数据中的每一个数据都加上10，得到一组新数据，则所得新数据的平均数和方差分别是（ ）

    A．12.8 3.6 B．2.8 13.6 C．12.8 13.6 D．13.6 12.8

    查看答案和解析>>

    同步练习册答案