
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
【答案】(1)![]() 不是指数数列,
不是指数数列,![]() 是指数数列,见解析;(2)见解析;(3)见解析
是指数数列,见解析;(2)见解析;(3)见解析
【解析】
(1)对数列![]() 、
、![]() ,验证
,验证![]() 与
与![]() ,
,![]() 与
与![]() 是否相等,由此判断出
是否相等,由此判断出![]() 、
、![]() 是不是指数数列.
是不是指数数列.
(2)利用累加法求得数列![]() 的通项公式,然后验证
的通项公式,然后验证![]() ,由此证得
,由此证得![]() 是指数数列.
是指数数列.
(3)首先根据指数数列的定义求得数列![]() 的通项公式,利用反证法,证得数列
的通项公式,利用反证法,证得数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
(1)对于数列![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 不是指数数列.
不是指数数列.
对于数列![]() ,对任意
,对任意![]() ,因为
,因为![]() ,所以
,所以![]() 是指数数列.
是指数数列.
(2)由题意,![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() ,公比为2的等比数列.所以
,公比为2的等比数列.所以![]() .
.
所以,![]()
![]() ,
,
即![]() 的通项公式为
的通项公式为![]() .所以
.所以![]() ,故
,故![]() 是指数数列.
是指数数列.
(3)因为数列![]() 是指数数列,故对于任意的
是指数数列,故对于任意的![]() ,有
,有![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以,
的等比数列,所以,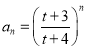 .
.
假设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 构成等差数列,不妨设
构成等差数列,不妨设![]() ,
,
则由![]() ,得
,得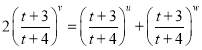 ,所以
,所以![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 是偶数,而
是偶数,而![]() 是偶数,
是偶数,![]() 是奇数,
是奇数,
故![]() 不能成立;
不能成立;
当![]() 为奇数时,
为奇数时,![]() 是偶数,而
是偶数,而![]() 是奇数,
是奇数,![]() 是偶数,
是偶数,
故![]() 也不能成立.
也不能成立.
所以,对任意![]() ,
,![]() 不能成立,
不能成立,
即数列![]() 的任意三项都不成构成等差数列.
的任意三项都不成构成等差数列.
(另证:因为对任意![]() ,
,![]() 一定是偶数,而
一定是偶数,而![]() 与
与![]() 为一奇一偶,故
为一奇一偶,故![]() 与
与![]() 也为一奇一偶,故等式右边一定是奇数,等式不能成立.)
也为一奇一偶,故等式右边一定是奇数,等式不能成立.)


科目:高中数学 来源: 题型:
【题目】青岛二中高一高二高三三个年级数学MT的学生人数分别为240人,240人,120人,现采用分层抽样的方法从中抽取5名同学参加团队内部举办的趣味数学比赛,再从5位同学中选出2名一等奖记A=“两名一等奖来自同一年级”,则事件A的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是__________________.
①命题“若x2-3x+2=0,则x=1”的逆否命题为:若x≠1,则x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:x∈R,使得x2+x+1<0,则非p:x∈R, 均有x2+x+1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A.一条直线与两个平行平面中的一个平行,则必与另一个平面平行
B.空间中两条直线要么平行,要么相交
C.空间中任意的三个点都能唯一确定一个平面
D.对于空间中任意两条直线,总存在平面与这两条直线都平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
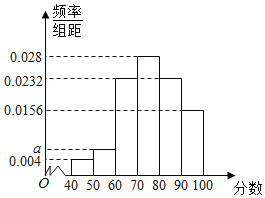
(1)求频率分布直方图中a的值;
(2)求这50名问卷评分数据的中位数;
(3)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com