
分析 求出线段PF的垂直平分线方程,联立$\left\{\begin{array}{l}{y=t}\\{y=\frac{2}{t}x+\frac{t}{2}}\end{array}\right.$,把x,y用含有t的代数式表示,消去参数t得答案;由题意可得,F为△ABC的重心,然后结合构造以F为重心的三角形可以构造无数个得答案.
解答 解:∵F(1,0),P(-1,t),∴线段PF的中点为(0,$\frac{t}{2}$),
线段PF的垂直平分线方程为y=$\frac{2}{t}x+\frac{t}{2}$,
联立$\left\{\begin{array}{l}{y=t}\\{y=\frac{2}{t}x+\frac{t}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{y=t}\\{x=\frac{{t}^{2}}{4}}\end{array}\right.$,
消去t得,y2=4x;
抛物线方程为y2=4x,A、B、C为曲线?上三点,当$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$时,F为△ABC的重心,
用如下办法构造△ABC,连接AF并延长至D,使FD=$\frac{1}{2}AF$,
当D在抛物线内部时,存在以D为中点的弦BC,则这样的三角形有无数个.
故答案为:y2=4x;无数.
点评 本题考查轨迹方程的求法,抛物线的定义及问题的转化能力,是中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,+∞) | C. | (-2,+∞) | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
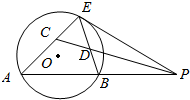 如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.
如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com