
【题目】已知函数f(x)=|x﹣ ![]() |+|x+
|+|x+ ![]() |,M为不等式f(x)<2的解集. (Ⅰ)求M;
|,M为不等式f(x)<2的解集. (Ⅰ)求M;
(Ⅱ)证明:当a,b∈M时,|a+b|<|1+ab|.
【答案】解:(I)当x<﹣ ![]() 时,不等式f(x)<2可化为:
时,不等式f(x)<2可化为: ![]() ﹣x﹣x﹣
﹣x﹣x﹣ ![]() <2, 解得:x>﹣1,
<2, 解得:x>﹣1,
∴﹣1<x<﹣ ![]() ,
,
当﹣ ![]() ≤x≤
≤x≤ ![]() 时,不等式f(x)<2可化为:
时,不等式f(x)<2可化为: ![]() ﹣x+x+
﹣x+x+ ![]() =1<2,
=1<2,
此时不等式恒成立,
∴﹣ ![]() ≤x≤
≤x≤ ![]() ,
,
当x> ![]() 时,不等式f(x)<2可化为:﹣
时,不等式f(x)<2可化为:﹣ ![]() +x+x+
+x+x+ ![]() <2,
<2,
解得:x<1,
∴ ![]() <x<1,
<x<1,
综上可得:M=(﹣1,1);
证明:(Ⅱ)当a,b∈M时,
(a2﹣1)(b2﹣1)>0,
即a2b2+1>a2+b2 ,
即a2b2+1+2ab>a2+b2+2ab,
即(ab+1)2>(a+b)2 ,
即|a+b|<|1+ab|
【解析】(I)分当x<﹣ ![]() 时,当﹣
时,当﹣ ![]() ≤x≤
≤x≤ ![]() 时,当x>
时,当x> ![]() 时三种情况,分别求解不等式,综合可得答案;(Ⅱ)当a,b∈M时,(a2﹣1)(b2﹣1)>0,即a2b2+1>a2+b2 , 配方后,可证得结论.
时三种情况,分别求解不等式,综合可得答案;(Ⅱ)当a,b∈M时,(a2﹣1)(b2﹣1)>0,即a2b2+1>a2+b2 , 配方后,可证得结论.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:方程![]() 有实根;
有实根;
(2)![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集为空集,求所有满足条件的实数
的解集为空集,求所有满足条件的实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成![]() 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.

(1)求实数![]() 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
(2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数![]() 若函数
若函数![]() ,利用上述性质,
,利用上述性质,
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求
时,求![]() 的单调递增区间
的单调递增区间![]() 只需判定单调区间,不需要证明
只需判定单调区间,不需要证明![]() ;
;
![]() Ⅱ
Ⅱ![]() 设
设![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求实数a的取值范围.
恰有四解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 关于函数
关于函数![]() 的性质,有以下四个推断:
的性质,有以下四个推断:
①![]() 的定义域是
的定义域是![]() ; ②
; ②![]() 的值域是
的值域是![]() ;
;
③![]() 是奇函数; ④
是奇函数; ④![]() 是区间
是区间![]() 上的增函数.
上的增函数.
其中推断正确的题号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R(公里) | ||
80≤R<150 | 150≤R<250 | R≥250 | |
纯电动乘用车 | 3.5万元/辆 | 5万元/辆 | 6万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
分组 | 频数 | 频率 |
80≤R<150 | 2 | 0.2 |
150≤R<250 | 5 | x |
R≥250 | y | z |
合计 | M | 1 |
(Ⅰ)求x,y,z,M的值;
(Ⅱ)若从这M辆纯电动乘用车中任选2辆,求选到的2辆车续驶里程都不低于150公里的概率;
(Ⅲ)若以频率作为概率,设X为购买一辆纯电动乘用车获得的补贴,求X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+alnx(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2(x1<x2),且不等式f(x1)≥mx2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四个小动物换座位,开始是鼠、猴、兔、猫分别坐在 1,2,3,4 号位子上(如图), 第一次前后排动物互换座位,第二次左右列动物互换座位,.....,这样交替进行下去,那么第 2013 次互换座位后,小兔的座位对应的是( )

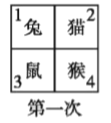
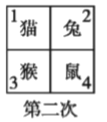
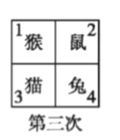
A. 编号 1 B. 编号 2 C. 编号 3 D. 编号 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com