练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图为一个几何体的三视图，则该几何体的外接球的表面积为（　　）
    A、4πB、8π
    C、12πD、16π
    考点：由三视图求面积、体积
    专题：空间位置关系与距离
    分析：如图所示，该几何体为四棱锥P-ABCD，其中PA⊥底面ABCD，底面ABCD是边长为2的正方形，PA=2．取PC的中点O，则点O是该几何体的外接球的球心．求出即可．
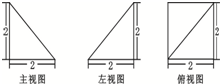
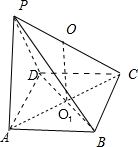    解答： 解：如图所示，该几何体为四棱锥P-ABCD，其中PA⊥底面ABCD，底面ABCD是边长为2的正方形，PA=2．
    取PC的中点O，则点O是该几何体的外接球的球心．
    OC=
    1
    2
    PC=
    1
    2
    		PA2+AC2
    =
    		3
    ．
    ∴该几何体的外接球的表面积=4πR2=12π．
    故选：C．
    点评：本题考查了四棱锥外接球的表面积、三视图的有关知识，考查了推理能力与计算能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的焦距和短轴长相等，且椭圆C过点（1，-
    		2
    2
    ）．过点P（0，2）的直线l交椭圆C于M、N两点．
    （1）求椭圆C的标准方程；
    （2）当△MON的面积最大时，求直线l 的方程，并求出此时面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给定下列命题：
    （1）在△ABC中，∠A＜∠B是cos2A＞cos2B的充要条件；
    （2）λ，μ为实数，若λ
    a
    =μ
    b
    ，则
    a
    与
    b
    共线；
    （3）若向量
    a
    ，
    b
    满足|
    a
    |=|
    b
    |，则
    a
    =
    b
    或
    a
    =-
    b
    ；
    （4）函数y=sin(2x+
    π
    3
    )sin(
    π
    6
    -2x)    的最小正周期是π；
    （5）若命题p为：
    1
    x-1
    ＞0，则?p：
    1
    x-1
    ≤0
    （6）由a1=1，an=3n-1，求出S1，S2，S3猜想出数列的前n项和Sn的表达式的推理是归纳推理．
    其中正确的命题的个数为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某三棱锥的三视图如图所示，这个三棱锥最长棱的棱长是（　　）
    A、1
    B、
    		2
    C、
    		3
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

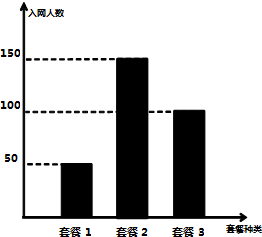    移动公司在国庆期间推出4G套餐，对国庆节当日办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元．国庆节当天参与活动的人数统计结果如图所示，现将频率视为概率．
    （1）求某人获得优惠金额不低于300元的概率；
    （2）若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选出两人，求这两人获得相等优惠金额的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x2-2x（x∈R），则f（x）的零点个数为（　　）个．
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC的内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，且c=2a，则sinB=（　　）
    A、
    1
    4
    B、
    3
    4
    C、
    		7
    4
    D、
    		2
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，M是BC的中点，AM=5，BC=6，则
    AB
    •
    AC
    等于（　　）
    A、9B、12C、16D、30

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在R上定义的函数f（x）是偶函数，且f（x）=f（2-x），若f（x）在区间x∈[1，2）是减函数，则函数 f（x）（　　）
    A、在区间[-2，-1]上是减函数，区间[3，4]上是增函数
    B、在区间[-2，-1]上是减函数，区间[3，4]上是减函数
    C、在区间[-2，-1]上是增函数，区间[3，4]上是增函数
    D、在区间[-2，-1]上是增函数，区间[3，4]上是减函数

    查看答案和解析>>

    同步练习册答案