
ЁОЬтФПЁПФГЕиМЖЪаЙВга![]() жабЇЩњЃЌЦфжага
жабЇЩњЃЌЦфжага![]() бЇЩњдк
бЇЩњдк![]() ФъЯэЪмСЫЁАЙњМвОЋзМЗіЦЖЁБеўВпЃЌдкЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњжаРЇФбГЬЖШЗжЮЊШ§ИіЕШДЮЃКвЛАуРЇФбЁЂКмРЇФбЁЂЬиБ№РЇФбЃЌЧвШЫЪ§жЎБШЮЊ
ФъЯэЪмСЫЁАЙњМвОЋзМЗіЦЖЁБеўВпЃЌдкЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњжаРЇФбГЬЖШЗжЮЊШ§ИіЕШДЮЃКвЛАуРЇФбЁЂКмРЇФбЁЂЬиБ№РЇФбЃЌЧвШЫЪ§жЎБШЮЊ![]() ЃЌЮЊНјвЛВНАяжњетаЉбЇЩњЃЌЕБЕиЪаеўИЎЩшСЂЁАзЈЯюНЬг§ЛљН№ЁБЃЌЖдетШ§ИіЕШДЮЕФРЇФббЇЩњУПФъУПШЫЗжБ№ВЙжњ
ЃЌЮЊНјвЛВНАяжњетаЉбЇЩњЃЌЕБЕиЪаеўИЎЩшСЂЁАзЈЯюНЬг§ЛљН№ЁБЃЌЖдетШ§ИіЕШДЮЕФРЇФббЇЩњУПФъУПШЫЗжБ№ВЙжњ![]() дЊЁЂ
дЊЁЂ![]() дЊЁЂ
дЊЁЂ![]() дЊ.ОМУбЇМвЕїВщЗЂЯжЃЌЕБЕиШЫОљПЩжЇХфФъЪеШыНЯЩЯвЛФъУПдіМг
дЊ.ОМУбЇМвЕїВщЗЂЯжЃЌЕБЕиШЫОљПЩжЇХфФъЪеШыНЯЩЯвЛФъУПдіМг![]() ЃЌвЛАуРЇФбЕФбЇЩњжага
ЃЌвЛАуРЇФбЕФбЇЩњжага![]() ЛсЭбЦЖЃЌЭбЦЖКѓНЋВЛдйЯэЪмЁАОЋзМЗіЦЖЁБеўВпЃЌКмРЇФбЕФбЇЩњга
ЛсЭбЦЖЃЌЭбЦЖКѓНЋВЛдйЯэЪмЁАОЋзМЗіЦЖЁБеўВпЃЌКмРЇФбЕФбЇЩњга![]() зЊЮЊвЛАуРЇФббЇЩњЃЌЬиБ№РЇФбЕФбЇЩњжага
зЊЮЊвЛАуРЇФббЇЩњЃЌЬиБ№РЇФбЕФбЇЩњжага![]() зЊЮЊКмРЇФббЇЩњ.ЯжЭГМЦСЫИУЕиМЖЪа
зЊЮЊКмРЇФббЇЩњ.ЯжЭГМЦСЫИУЕиМЖЪа![]() ФъЕН
ФъЕН![]() ФъЙВ
ФъЙВ![]() ФъЕФШЫОљПЩжЇХфФъЪеШыЃЌЖдЪ§ОнГѕВНДІРэКѓЕУЕНСЫШчЭМЫљЪОЕФЩЂЕуЭМКЭБэжаЭГМЦСПЕФжЕЃЌЦфжаФъЗн
ФъЕФШЫОљПЩжЇХфФъЪеШыЃЌЖдЪ§ОнГѕВНДІРэКѓЕУЕНСЫШчЭМЫљЪОЕФЩЂЕуЭМКЭБэжаЭГМЦСПЕФжЕЃЌЦфжаФъЗн![]() ШЁ
ШЁ![]() ЪБДњБэ
ЪБДњБэ![]() ФъЃЌ
ФъЃЌ![]() ШЁ
ШЁ![]() ЪБДњБэ
ЪБДњБэ![]() ФъЃЌЁЁвРДЫРрЭЦЃЌЧв
ФъЃЌЁЁвРДЫРрЭЦЃЌЧв![]() гы
гы![]() ЃЈЕЅЮЛЃКЭђдЊЃЉНќЫЦТњзуЙиЯЕЪН
ЃЈЕЅЮЛЃКЭђдЊЃЉНќЫЦТњзуЙиЯЕЪН![]() .ЃЈ
.ЃЈ![]() ФъжС
ФъжС![]() ФъИУЪажабЇЩњШЫЪ§ДѓжТБЃГжВЛБфЃЉ
ФъИУЪажабЇЩњШЫЪ§ДѓжТБЃГжВЛБфЃЉ
|
|
|
|
|
|

ЃЈ1ЃЉЙРМЦИУЪа![]() ФъШЫОљПЩжЇХфФъЪеШыЮЊЖрЩйЭђдЊЃП
ФъШЫОљПЩжЇХфФъЪеШыЮЊЖрЩйЭђдЊЃП
ЃЈ2ЃЉЪдЮЪИУЪа![]() ФъЕФЁАзЈЯюНЬг§ЛљН№ЁБЕФВЦеўдЄЫуДѓдМЮЊЖрЩйЭђдЊЃП
ФъЕФЁАзЈЯюНЬг§ЛљН№ЁБЕФВЦеўдЄЫуДѓдМЮЊЖрЩйЭђдЊЃП
ИНЃКЖдгквЛзщОпгаЯпадЯрЙиЙиЯЕЕФЪ§Он![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЦфЛиЙщжБЯпЗНГЬ
ЃЌЦфЛиЙщжБЯпЗНГЬ![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ ЃЌ
ЃЌ![]() .
.
ЁОД№АИЁП(1) ![]() ;(2)1624ЭђдЊ.
;(2)1624ЭђдЊ.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнБэжаЪ§ОнЃЌЧѓГі![]() ЃЌДњШыЙЋЪНЧѓжЕЃЌДгЖјЕУЕНЛиЙщжБЯпЗНГЬЃЌДњШы
ЃЌДњШыЙЋЪНЧѓжЕЃЌДгЖјЕУЕНЛиЙщжБЯпЗНГЬЃЌДњШы![]() МДПЩЃЛ
МДПЩЃЛ
ЃЈ2ЃЉЭЈЙ§гЩЬтвтжЊ![]() ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЙВ
ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЙВ![]() ШЫ.вЛАуРЇФбЁЂКмРЇФбЁЂЬиБ№РЇФбЕФжабЇЩњвРДЮга
ШЫ.вЛАуРЇФбЁЂКмРЇФбЁЂЬиБ№РЇФбЕФжабЇЩњвРДЮга![]() ШЫЁЂ
ШЫЁЂ![]() ШЫЁЂ
ШЫЁЂ![]() ШЫЃЌАДеедіГЄБШР§ЙиЯЕЧѓНт2017ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЃЌМДПЩЕУВЦеўдЄЫу.
ШЫЃЌАДеедіГЄБШР§ЙиЯЕЧѓНт2017ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЃЌМДПЩЕУВЦеўдЄЫу.
ЯъНтЃКЃЈ1ЃЉвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() .
.
Ыљвд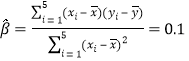 ЃЌ
ЃЌ
![]() ЃЌЫљвд
ЃЌЫљвд![]() .
.
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ФъШЫОљПЩжЇХфФъЪеШы
ФъШЫОљПЩжЇХфФъЪеШы![]() ЃЈЭђдЊЃЉ.
ЃЈЭђдЊЃЉ.
ЃЈ2ЃЉгЩЬтвтжЊ![]() ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЙВ
ФъЪБИУЪаЯэЪмЁАЙњМвОЋзМЗіЦЖЁБеўВпЕФбЇЩњЙВ![]() ШЫ.
ШЫ.
вЛАуРЇФбЁЂКмРЇФбЁЂЬиБ№РЇФбЕФжабЇЩњвРДЮга![]() ШЫЁЂ
ШЫЁЂ![]() ШЫЁЂ
ШЫЁЂ![]() ШЫЃЌ
ШЫЃЌ![]() ФъШЫОљПЩжЇХфЪеШыБШ
ФъШЫОљПЩжЇХфЪеШыБШ![]() ФъдіГЄ
ФъдіГЄ![]() .
.
Ыљвд![]() ФъИУЪаЬиБ№РЇФбЕФжабЇЩњга
ФъИУЪаЬиБ№РЇФбЕФжабЇЩњга![]() ШЫЃЌ
ШЫЃЌ
КмРЇФбЕФбЇЩњга![]() ШЫЃЌ
ШЫЃЌ
вЛАуРЇФбЕФбЇЩњга![]() ШЫ.
ШЫ.
Ыљвд![]() ФъЕФЁАзЈЯюНЬг§ЛљН№ЁБЕФВЦеўдЄЫуДѓдМЮЊ
ФъЕФЁАзЈЯюНЬг§ЛљН№ЁБЕФВЦеўдЄЫуДѓдМЮЊ![]() ЃЈЭђдЊЃЉ.
ЃЈЭђдЊЃЉ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкRЩЯЕФКЏЪ§fЃЈxЃЉТњзуfЃЈЉxЃЉ=ЉfЃЈxЃЉЃЌfЃЈxЉ2ЃЉ=fЃЈx+2ЃЉЃЌЧвxЁЪЃЈЉ1ЃЌ0ЃЉЪБЃЌfЃЈxЃЉ=2x+ ![]() ЃЌдђfЃЈlog220ЃЉ=ЃЈ ЃЉ
ЃЌдђfЃЈlog220ЃЉ=ЃЈ ЃЉ
A.Љ1
B.![]()
C.1
D.Љ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгШЋаЃВЮМгЪ§бЇОКШќЕФбЇЩњЕФЪдОэжаГщШЁвЛИібљБОЃЌПМВьОКШќЕФГЩМЈЗжВМЧщПіЃЌНЋбљБОЗжГЩ5зщЃЌЛцГЩЦЕТЪЗжВМжБЗНЭМЃЌЭМжаДгзѓЕНгвИїаЁзщЕФаЁГЄЗНаЮЕФИпжЎБШЮЊ1ЃК3ЃК6ЃК4ЃК2ЃЌзюгвБпвЛзщЦЕЪ§ЪЧ6ЃЌЧыНсКЯжБЗНЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉбљБОЕФШнСПЪЧЖрЩйЃП
ЃЈ2ЃЉСаГіЦЕТЪЗжВМБэЃЛ
ЃЈ3ЃЉЙРМЦетДЮОКШќжаЃЌГЩМЈИпгк60ЗжЕФбЇЩњеМзмШЫЪ§ЕФАйЗжБШЃЛ
ЃЈ4ЃЉГЩМЈТфдкФФИіЗЖЮЇФкЕФШЫЪ§зюЖрЃПВЂЧѓГіИУаЁзщЕФЦЕЪ§ЃЌЦЕТЪ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШ§РтзЖABCDжаЃЌBCЁЭCDЃЌRtЁїBCDаББпЩЯЕФИпЮЊ1ЃЌШ§РтзЖABCDЕФЭтНгЧђЕФжБОЖЪЧABЃЌШєИУЭтНгЧђЕФБэУцЛ§ЮЊ16ІаЃЌдђШ§РтзЖABCDЬхЛ§ЕФзюДѓжЕЮЊЃЈ ЃЉ
A.![]()
B.![]()
C.1
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтИпвЛЪЕбщАрЕФЪ§бЇГЩМЈ,ВЩгУГщбљЕїВщЕФЗНЪН,ЛёШЁСЫ![]() ЮЛбЇЩњдкЕквЛбЇЦкФЉЕФЪ§бЇГЩМЈЪ§Он,бљБОЭГМЦНсЙћШчЯТБэЃК
ЮЛбЇЩњдкЕквЛбЇЦкФЉЕФЪ§бЇГЩМЈЪ§Он,бљБОЭГМЦНсЙћШчЯТБэЃК
Зжзщ | ЦЕЪ§ | ЦЕТЪ |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
КЯМЦ |
|
|
(1)Чѓ![]() ЕФжЕКЭЪЕбщАрЪ§бЇЦНОљЗжЕФЙРМЦжЕЃЛ
ЕФжЕКЭЪЕбщАрЪ§бЇЦНОљЗжЕФЙРМЦжЕЃЛ
(2)ШчЙћгУЗжВуГщбљЕФЗНЗЈДгЪ§бЇГЩМЈаЁгк![]() ЗжЕФбЇЩњжаГщШЁ
ЗжЕФбЇЩњжаГщШЁ![]() УћбЇЩњ,дйДгет
УћбЇЩњ,дйДгет![]() УћбЇЩњжабЁ
УћбЇЩњжабЁ![]() ШЫ,ЧѓжСЩйгавЛИібЇЩњЕФЪ§бЇГЩМЈЪЧдк
ШЫ,ЧѓжСЩйгавЛИібЇЩњЕФЪ§бЇГЩМЈЪЧдк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЃК
ЃК ![]() ЃЌКЭСНЕу
ЃЌКЭСНЕу![]() ЃЈ0,1ЃЉЃЌ
ЃЈ0,1ЃЉЃЌ![]() ЃЈ-1,0ЃЉЃЌИјГіШчЯТНсТлЃК
ЃЈ-1,0ЃЉЃЌИјГіШчЯТНсТлЃК
ЂйВЛТл![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ ![]() гы
гы![]() ЖМЛЅЯрДЙжБЃЛ
ЖМЛЅЯрДЙжБЃЛ
ЂкЕБ![]() БфЛЏЪБЃЌ
БфЛЏЪБЃЌ ![]() гы
гы![]() ЗжБ№ОЙ§ЖЈЕуAЃЈ0,1ЃЉКЭBЃЈ-1,0ЃЉЃЛ
ЗжБ№ОЙ§ЖЈЕуAЃЈ0,1ЃЉКЭBЃЈ-1,0ЃЉЃЛ
ЂлВЛТл![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ ![]() гы
гы![]() ЖМЙигкжБЯп
ЖМЙигкжБЯп![]() ЖдГЦЃЛ
ЖдГЦЃЛ
ЂмШчЙћ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓжЕЪЧ1ЃЛ
ЕФзюДѓжЕЪЧ1ЃЛ
ЦфжаЃЌЫљгае§ШЗЕФНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
A. 1 B. 2 C. 3 D. 4.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
(1)Чѓf(2)ЃЌf(x)ЃЛ
(2)жЄУїЃККЏЪ§f(x)дк[1ЃЌ17]ЩЯЮЊдіКЏЪ§ЃЛ
(3)ЪдЧѓКЏЪ§f(x)дк[1ЃЌ17]ЩЯЕФзюДѓжЕКЭзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшРыаФТЪЮЊ ![]() ЕФЭждВEЃК
ЕФЭждВEЃК ![]() +
+ ![]() =1ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЮЊF1 ЃЌ F2 ЃЌ ЕуPЪЧEЩЯвЛЕуЃЌPF1ЁЭPF2 ЃЌ ЁїPF1F2ФкЧадВЕФАыОЖЮЊ
=1ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЮЊF1 ЃЌ F2 ЃЌ ЕуPЪЧEЩЯвЛЕуЃЌPF1ЁЭPF2 ЃЌ ЁїPF1F2ФкЧадВЕФАыОЖЮЊ ![]() Љ1ЃЎ
Љ1ЃЎ
ЃЈ1ЃЉЧѓEЕФЗНГЬЃЛ
ЃЈ2ЃЉОиаЮABCDЕФСНЖЅЕуCЁЂDдкжБЯпy=x+2ЃЌAЁЂBдкЭждВEЩЯЃЌШєОиаЮABCDЕФжмГЄЮЊ ![]() ЃЌЧѓжБЯпABЕФЗНГЬЃЎ
ЃЌЧѓжБЯпABЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФжааФдкзјБъдЕуЃЌНЙЕудк
ЕФжааФдкзјБъдЕуЃЌНЙЕудк![]() жсЩЯЃЌЭждВ
жсЩЯЃЌЭждВ![]() ЩЯЕФЕуЕННЙЕуОрРыЕФзюДѓжЕЮЊ3ЃЌзюаЁжЕЮЊ1.
ЩЯЕФЕуЕННЙЕуОрРыЕФзюДѓжЕЮЊ3ЃЌзюаЁжЕЮЊ1.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЃК
ЃК ![]() гыЭждВ
гыЭждВ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЈ
СНЕуЃЈ![]() ЃЌ
ЃЌ ![]() ВЛЪЧзѓгвЖЅЕуЃЉЃЌЧввд
ВЛЪЧзѓгвЖЅЕуЃЉЃЌЧввд![]() ЮЊжБОЖЕФдВЙ§ЭждВ
ЮЊжБОЖЕФдВЙ§ЭждВ![]() ЕФгвЖЅЕу.ЧѓжЄЃКжБЯп
ЕФгвЖЅЕу.ЧѓжЄЃКжБЯп![]() Й§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъ.
Й§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com