Question

已知(＋ax²)²ⁿ的展开式记为R，(3x－1)ⁿ的展开式记为T.已知R的奇数项的二项式系数的和比T的偶数项的二项式系数的和大496.

(1)求R中二项式系数最大的项；

(2)求R中的有理项；

(3)确定实数a的值，使R与T中有相同的项．

Answer 1

【解】　由题意2^2n－1－2^n－1＝496，解得n＝5.

(1)(＋ax²)¹⁰的展开式中第6项的二项式系数最大，结果为C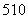()⁵·(ax²)⁵＝252a⁵x.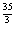

(2)R展开式的通项公式T_r＋1＝C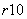()^10－r(ax²)^r＝C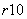a^rx＋2r

由＋2r∈Z，且0≤r≤10，所以r＝1，4，7，10.

故R中的有理项为T₂＝C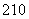a²x⁵＝45a²x⁵，

T₅＝C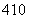a⁴x¹⁰＝210a⁴x¹⁰，

T₈＝C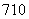a⁷x¹⁵＝120a⁷x¹⁵，T₁₁＝C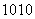a¹⁰x²⁰＝a¹⁰x²⁰.

(3)T展开式的通项公式S_t＋1＝C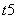(3x)^5－t(－1)^t＝C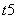(－1)t3⁵－tx^5－t，

由＋2r＝5－t，即3t＝5(1－r)，

所以r＝1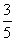－t.又0≤r≤10，0≤－1≤5，所以t＝0.

当t＝0时，r＝1，此时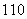Ca＝C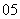3⁵·(－1)⁰，a＝.

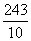故当a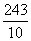＝时，R，T中有相同的项．