练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5，40]中，其频率分布直方图如图所示．从抽样的100根棉花纤维中任意抽取一根，则其棉花纤维的长度小于20mm的概率为　　．


    【解析】根据题意，棉花纤维的长度小于20mm的有三组，

    [5，10）这一组的频率为5×0.01=0.05，有100×0.05=5根棉花纤维在这一组，

    [10，15）这一组的频率为5×0.01=0.05，有100×0.05=5根棉花纤维在这一组，

    [15，20）这一组的频率为5×0.04=0.2，有100×0.2=20根棉花纤维在这一组，

    则长度小于20mm的有5+5+20=30根，

    则从抽样的100根棉花纤维中任意抽取一根，其长度小于20mm的概率为=；

    故答案为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天．

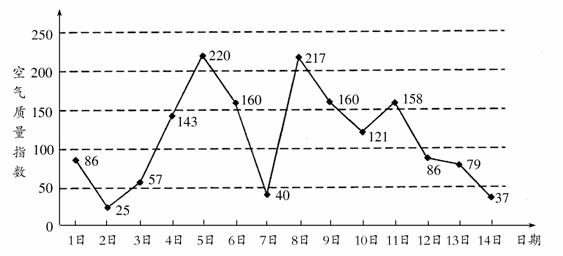
    (1)求此人到达当日空气重度污染的概率；

    (2)设X是此人停留期间空气质量优良的天数，求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知(＋ax2)2n的展开式记为R，(3x－1)n的展开式记为T.已知R的奇数项的二项式系数的和比T的偶数项的二项式系数的和大496.

    (1)求R中二项式系数最大的项；

    (2)求R中的有理项；

    (3)确定实数a的值，使R与T中有相同的项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A={0，1，2}，B={x|x=2a，a∈A}，则A∩B中元素的个数为（　　）

    　

    A．

    0

    B．

    1

    C．

    2

    D．

    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知、是圆上的两个点，是线段上的动点，当的面积最大时，则的最大值是（     ）

    A.       B.                         C.                        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：           性别与读营养说明列联表

    男

    女

    总计

    读营养说明

    16

    8

    24

    不读营养说明

    4

    12

    16

    总计

    20

    20

    40

    ⑴根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？

    ⑵从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数的分布列及其均值（即数学期望）．

    （注：，其中为样本容量．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知全集U={1，2，3，4，5，6，7，8}，M={1，3，5，7}，N={5，6，7}，则∁U（M∪N）=（　　）

    　

    A．

    {5，7}

    B．

    {2，4}

    C．

    {2，4，8}

    D．

    {1，3，5，6，7}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆的左顶点为，过原点的直线交椭圆于两点，若，，则椭圆方程为（    ）

    A．　　　　B．　　　C．　　　　　D．

    查看答案和解析>>

    同步练习册答案