【题目】（本小题满分12分）贵广高速铁路自贵阳北站起，经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站. 其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站. 记者对广东省内的6个车站随机抽取3个进行车站服务满意度调查.
（1）求抽取的车站中含有佛山市内车站（包括三水南站和佛山西站）的概率；
（2）设抽取的车站中含有肇庆市内车站（包括怀集站、广宁站、肇庆东站）个数为X，求X的分布列及其均值（即数学期望）.
【答案】（1）
；（2）
【解析】
试题（1）求随机变量的分布列的主要步骤：一是明确随机变量的取值，并确定随机变量服从何种概率分布；二是求每一个随机变量取值的概率，三是列成表格；（2）求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确；（3）求解离散随机变量分布列和方差，首先要理解问题的关键，其次要准确无误的找出随机变量的所有可能值，计算出相对应的概率，写成随机变量的分布列，正确运用均值、方差公式进行计算.
试题解析：（1）设“抽取的车站中含有佛山市内车站”为事件A，
则
（4分）
（2）X的可能取值为0，1，2，3 （5分）
，
， （7分）
，
， （9分）
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
（10分）
X的数学期望
. （12分）
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，PD//MA，MA⊥AD，PM⊥平面CDM，MA=AD
PD=1.
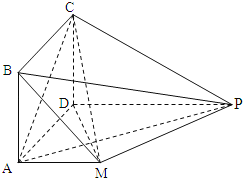
（1）求证：平面ABCD⊥平面AMPD；
（2）求三棱锥A﹣CMP的高.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的中心在原点，焦点在
轴上，离心率等于
，它的一个顶点恰好在抛物线
的准线上．
（Ⅰ）求椭圆的标准方程．
（Ⅱ）点
，
在椭圆上，
，
是椭圆上位于直线
两侧的动点．
（i）若直线
的斜率为
，求四边形
面积的最大值．
（ii）当，运动时，满足
，试问直线的斜率是否为定值，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
的焦点是椭圆
： 
（
）的顶点，且椭圆与双曲线的离心率互为倒数.
（Ⅰ）求椭圆
的方程；
（Ⅱ）设动点
， 
在椭圆
上，且
，记直线
在
轴上的截距为
，求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为促进义务教育的均衡发展，各地实行免试就近入学政策，某地区随机调查了
人，他们年龄的频数分布及赞同“就近入学”人数如表：
年龄 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞同 |
|
|
|
|
|
|
（Ⅰ）在该样本中随机抽取
人，求至少
人支持“就近入学”的概率；
（Ⅱ）若对年龄在
，
的被调查人中各随机选取两人进行调查，记选中的
人支持“就近入学”人数为
，求随机变量的分布列及数学期望。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，
．
（1）若函数f（x）在
处有极值，求函数f（x）的最大值；
（2）是否存在实数b，使得关于x的不等式
在
上恒成立？若存在，求出b的取值范围；若不存在，说明理由；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
