练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝sinxcosx－cos2x－，x∈R.

    (1)求函数f(x)的最小值和最小正周期；

    (2)已知△ABC内角A、B、C的对边分别为a、b、c，且c＝3，f(C)＝0，若向量m＝(1，sinA)与n＝(2，sinB)共线，求a、b的值．


    　(1)f(x)＝sinxcosx－cos2x－＝sin2x－cos2x－1＝sin(2x－)－1，

    ∴f(x)的最小值是－2，最小正周期为π.

    (2)∵f(C)＝sin(2C－)－1＝0，即sin(2C－)＝1，

    ∵0<C<π，－<2C－<，

    ∴2C－＝，∴C＝.

    ∵m与n共线，∴sinB－2sinA＝0.

    由正弦定理＝，得b＝2a，①

    ∵c＝3，由余弦定理得，9＝a2＋b2－2abcos，②

    解方程组①②得，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知角α是第n(n＝1、2、3、4)象限的角，问是第几象限的角？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知m＝(asinx，cosx)，n＝(sinx，bsinx)，其中a，b，x∈R.若f(x)＝m·n满足f(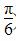)＝2，且f(x)的导函数f ′(x)的图象关于直线x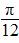＝对称．

    (1)求a，b的值；

    (2)若关于x的方程f(x)＋log2k＝0在区间[0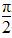，]上总有实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝cos2ax－sin2ax的最小正周期为π，则a的值是(　　)

    A．－1                                                          B．1

    C．2                                                             D．±1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    要使sinα－cosα＝有意义，则m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝asin(π－2x)＋bsin(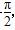＋2x)，其中a，b∈R，ab≠0，若f(x)≤|f(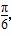)|对一切x∈R恒成立，则

    ①f()＝0

    ②f(x)的周期为2π

    ③f(x)既不是奇函数也不是偶函数

    ④存在经过点(a，b)的直线与函数f(x)的图象不相交

    以上结论正确的是________．(写出所有正确结论的编号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l：xtanα－y－3tanβ＝0的斜率为2，在y轴上的截距为1，则tan(α＋β)＝(　　)

    A．－                                                       B.

    C.                                                             D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面几何里，有勾股定理：“设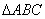的两边AB、AC互相垂直，则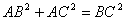。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直，则                             ”。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3 t、B原料2 t,生产每吨乙产品要用A原料1 t、B原料3 t.销售每吨甲产品可获得利润5万元,销售每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13t、B原料不超过18t.求该企业可获得的最大利润.

    查看答案和解析>>

    同步练习册答案