
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据绘制的散点图能够看出可用线性回归模型![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);
(2)建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:(1)样本![]() 相关系数
相关系数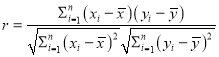 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为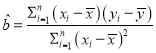 ,
,![]() .
.
【答案】(1)散点图见解析,相关系数的值接近于1,说明变量![]() 与
与![]() 的线性相关性很强;(2)
的线性相关性很强;(2)![]() ,24.70万元
,24.70万元
【解析】
(1)根据数据绘制散点图,从散点图看出这些点是否大致分布在一条直线附近即可;计算![]() ,
,![]() ,求出相关系数,判断两变量线性相关性的强弱;
,求出相关系数,判断两变量线性相关性的强弱;
(2)计算求出回归方程,利用方程求出对应![]() 的取值范围即可.
的取值范围即可.
解:(1)根据数据绘制散点图如下,
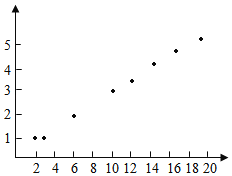
从散点图可以看出这些点大致分布在一条直线附近,并且在逐步上升,
所以可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
计算![]() ,
,
![]() ,
,
∴相关系数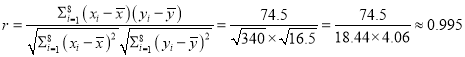 ,
,
由相关系数的值接近于1,说明变量![]() 与
与![]() 的线性相关性很强;
的线性相关性很强;
(2)计算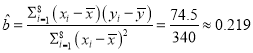 ,
,
![]() ,
,
∴![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ;
;
令![]() ,解得
,解得![]() ;
;
即实现产品销量超6万件,预测至少需要投入促销费用24.70万元.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生文艺部6名成员(4男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
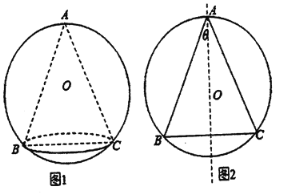
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
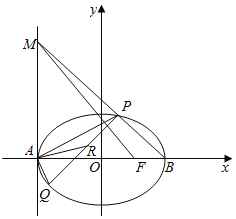
【题目】已知椭圆C:![]() 的左右顶点为A、B,右焦点为F,一条准线方程是
的左右顶点为A、B,右焦点为F,一条准线方程是![]() ,短轴一端点与两焦点构成等边三角形,点P、Q为椭圆C上异于A、B的两点,点R为PQ的中点
,短轴一端点与两焦点构成等边三角形,点P、Q为椭圆C上异于A、B的两点,点R为PQ的中点
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 直线PB交直线
直线PB交直线![]() 于点M,记直线PA的斜率为
于点M,记直线PA的斜率为![]() ,直线FM的斜率为
,直线FM的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
![]() 若
若![]() ,求直线AR的斜率的取值范围.
,求直线AR的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sin![]() cos x+
cos x+![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若函数g(x)=f(x)-m区间在![]() 上有两个不同的零点x1,x2,求实数m的取值范围,并计算tan(x1+x2)的值.
上有两个不同的零点x1,x2,求实数m的取值范围,并计算tan(x1+x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() (含端点)上的一个动点.设
(含端点)上的一个动点.设![]() ,
,![]() ,对于函数
,对于函数![]() ,下列描述正确的是( )
,下列描述正确的是( )
A.![]() 的最大值和
的最大值和![]() 无关B.
无关B.![]() 的最小值和
的最小值和![]() 无关
无关
C.![]() 的值域和
的值域和![]() 无关D.
无关D.![]() 在其定义域上的单调性和
在其定义域上的单调性和![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点是
的左、右焦点是![]() ,左右顶点是
,左右顶点是![]() ,离心率是
,离心率是![]() ,过
,过![]() 的直线与椭圆交于两点P、Q(不是左、右顶点),且
的直线与椭圆交于两点P、Q(不是左、右顶点),且![]() 的周长是
的周长是![]() ,
,
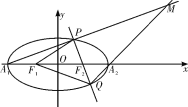
直线![]() 与
与![]() 交于点M.
交于点M.
(1)求椭圆的方程;
(2)(ⅰ)求证直线![]() 与
与![]() 交点M在一条定直线l上;
交点M在一条定直线l上;
(ⅱ)N是定直线l上的一点,且PN平行于x轴,证明:![]() 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com