
【题目】已知椭圆![]() 的左、右焦点是
的左、右焦点是![]() ,左右顶点是
,左右顶点是![]() ,离心率是
,离心率是![]() ,过
,过![]() 的直线与椭圆交于两点P、Q(不是左、右顶点),且
的直线与椭圆交于两点P、Q(不是左、右顶点),且![]() 的周长是
的周长是![]() ,
,
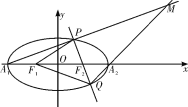
直线![]() 与
与![]() 交于点M.
交于点M.
(1)求椭圆的方程;
(2)(ⅰ)求证直线![]() 与
与![]() 交点M在一条定直线l上;
交点M在一条定直线l上;
(ⅱ)N是定直线l上的一点,且PN平行于x轴,证明:![]() 是定值.
是定值.
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据绘制的散点图能够看出可用线性回归模型![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);
(2)建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:(1)样本![]() 相关系数
相关系数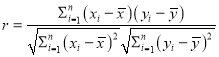 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为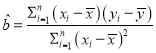 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为4的正三角形ABC的边AB、AC上分别有两点D、E,DE//BC且DE=3,现将△ABC沿DE折成直二面角A﹣DE﹣B,在空间中取一点F使得ADBF为平行四边形,连接AC、FC得六面体ABCEDF,G是BC边上动点.
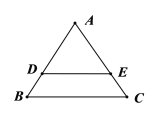
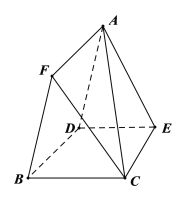
(1)若EG//平面ACF,求CG的长;
(2)若G为BC中点,求二面角G﹣AE﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
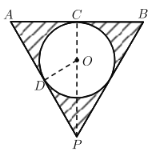
【题目】有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为![]() 的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足,当点
为垂足,当点![]() 在圆
在圆![]() 上运动时,设线段
上运动时,设线段![]() 中点
中点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)试问在![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,且以
对称,且以![]() 为直径的圆恰好经过坐标原点?若存在,求出直线
为直径的圆恰好经过坐标原点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com