
【题目】为响应市政府提出的以新旧动能转换为主题的发展战略,某公司花费100万元成本购买了1套新设备用于扩大生产,预计该设备每年收入100万元,第一年该设备的各种消耗成本为8万元,且从第二年开始每年比上一年消耗成本增加8万元.
(1)求该设备使用x年的总利润y(万元)与使用年数x(x∈N*)的函数关系式(总利润=总收入﹣总成本);
(2)这套设备使用多少年,可使年平均利润最大?并求出年平均利润的最大值.
【答案】(1)![]() ;(2)这套设备使用5年,可使年平均利润最大,最大利润为56万元
;(2)这套设备使用5年,可使年平均利润最大,最大利润为56万元
【解析】
(1)求出![]() 年的总收入及消耗等总费用,可得总利润
年的总收入及消耗等总费用,可得总利润![]() 与使用年数
与使用年数![]()
![]() 的函数关系;
的函数关系;
(2)年平均利润为![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
(1)由题意知,x年总收入为100x万元,
x年消耗成本总费用为8(1+2+3+…+x)=4x(1+x)万元,
∴总利润y=100x﹣4x(x+1)﹣100,x∈N*,即y=﹣4x2+96x﹣100,x∈N*;
(2)年平均利润为![]() ,∵x>0,
,∵x>0,
∴![]() 4(x
4(x![]() )+96
)+96![]() 56,
56,
当且仅当x![]() ,即x=5时取“=”号.
,即x=5时取“=”号.
∴当设备使用5年时,年平均利润最大.
答:这套设备使用5年,可使年平均利润最大,最大利润为56万元.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,F关于原点的对称点为P,过F作
的焦点为F,F关于原点的对称点为P,过F作![]() 轴的垂线交抛物线于M,N两点,给出下列三个结论:
轴的垂线交抛物线于M,N两点,给出下列三个结论:
①![]() 必为直角三角形;
必为直角三角形;
②直线![]() 必与抛物线相切;
必与抛物线相切;
③![]() 的面积为
的面积为![]() .其中正确的结论是___.
.其中正确的结论是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则直线
,则直线![]() 不一定平行于直线
不一定平行于直线![]()
B. 若平面![]() 不垂直于平面
不垂直于平面![]() ,则
,则![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 若平面![]() 平面
平面![]() ,则
,则![]() 内一定不存在直线平行于平面
内一定不存在直线平行于平面![]()
D. 若平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,则
,则![]() 一定垂直于平面
一定垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形![]() 中(图1),
中(图1),![]() 为
为![]() 的中点,
的中点,![]() ,且
,且![]() ,现将此平面四边形沿
,现将此平面四边形沿![]() 折起,使得二面角
折起,使得二面角![]() 为直二面角,得到一个多面体,
为直二面角,得到一个多面体,![]() 为平面
为平面![]() 内一点,且
内一点,且![]() 为正方形(图2),
为正方形(图2),![]() 分别为
分别为![]() 的中点.
的中点.
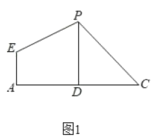
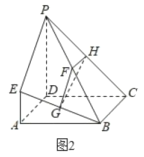
(1)求证:平面![]() //平面
//平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且它的焦距是短轴长的
,且它的焦距是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的方程.
的方程.
(2)若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点(
上的两个动点(![]() ,
,![]() 两点不关于
两点不关于![]() 轴对称),
轴对称),![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,问是否存在非零常数
,问是否存在非零常数![]() ,使当
,使当![]() 时,
时,![]() 的面积
的面积![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
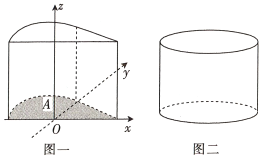
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,公差为
,公差为![]()
![]() 若
若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
![]() 是否存在d,n使
是否存在d,n使![]() 成立?若存在,试找出所有满足条件的d,n的值,并求出数列
成立?若存在,试找出所有满足条件的d,n的值,并求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com