
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
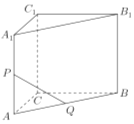
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若直三棱柱![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
【解析】
(1)以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴正方向建立空间直角坐标系,分别求出异面直线
轴正方向建立空间直角坐标系,分别求出异面直线![]() 与
与![]() 的方向向量,代入向量夹角公式,即可求出异面直线
的方向向量,代入向量夹角公式,即可求出异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)连接![]() .由
.由![]() ,由已知中,
,由已知中,![]() 是
是![]() 的中点,
的中点,![]() 面
面![]() ,我们根据等腰三角形“三线合一”的性质及线面垂直的性质,即可得到
,我们根据等腰三角形“三线合一”的性质及线面垂直的性质,即可得到![]() ,
,![]() ,进而根据线面垂直的判定定理,得到
,进而根据线面垂直的判定定理,得到![]() 面
面![]() ,故
,故![]() 即为四棱锥
即为四棱锥![]() 的高,求出棱锥的底面面积,代入棱锥体积公式,即可得到答案.
的高,求出棱锥的底面面积,代入棱锥体积公式,即可得到答案.
(1)以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 为
为![]() 轴正方向建立空间直角坐标系.不妨设
轴正方向建立空间直角坐标系.不妨设![]() .
.
依题意,可得点的坐标![]() ,
,
于是![]() ,由
,由![]() ,
,
则异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
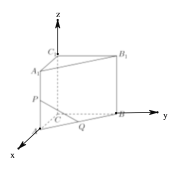
(2)连接![]() .由
.由![]() ,
,![]() 是
是![]() 的中点,得
的中点,得![]() ;
;
由![]() 面
面![]() ,
,![]() 面
面![]() ,得
,得![]() .
.
又![]() ,因此
,因此![]() 面
面![]() ,
,
由直三棱柱![]() 的体积为
的体积为![]() .可得
.可得![]() .
.
所以,四棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,
上,![]() .动点
.动点![]() 从
从![]() 出发沿直线向
出发沿直线向![]() 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点
运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点![]() 第一次碰到
第一次碰到![]() 时,
时,![]() 与正方形的边碰撞的次数为( )
与正方形的边碰撞的次数为( )
A. 4B. 3C. 8D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉中市2019年油菜花节在汉台区举办,组委会将甲、乙等6名工作人员分配到两个不同的接待处负责参与接待工作,每个接待处至少2人,则甲、乙两人不在同一接待处的分配方法共有( )
A. 12种B. 22种C. 28种D. 30种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上.
的图像上.
(1)证明:当![]() 时,
时,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() 为数列
为数列 的前n项的积,若不等式
的前n项的积,若不等式![]() 对一切
对一切![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)集合![]() ,
,![]() 或
或![]() ,对于任意
,对于任意![]() ,定义
,定义![]() ,对任意
,对任意![]() ,定义
,定义![]() ,记
,记![]() 为集合
为集合![]() 的元素个数,求
的元素个数,求![]() 的值;
的值;
(2)在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)已知当![]() 时,有
时,有![]() ,根据此信息,若对任意
,根据此信息,若对任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为圆
为圆![]() 上一动点,圆心
上一动点,圆心![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 只有一个公共点
只有一个公共点![]() ,且点
,且点![]() 在第二象限,过坐标原点
在第二象限,过坐标原点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M为△ABC的中线AD的中点,过点M的直线分别交线段AB、AC于点P、Q两点,设![]() ,
,![]() ,记
,记![]() .
.
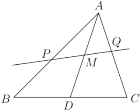
(1)求![]() 的值;
的值;
(2)求函数![]() 的解析式(指明定义域);
的解析式(指明定义域);
(3)设![]() ,
,![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应市政府提出的以新旧动能转换为主题的发展战略,某公司花费100万元成本购买了1套新设备用于扩大生产,预计该设备每年收入100万元,第一年该设备的各种消耗成本为8万元,且从第二年开始每年比上一年消耗成本增加8万元.
(1)求该设备使用x年的总利润y(万元)与使用年数x(x∈N*)的函数关系式(总利润=总收入﹣总成本);
(2)这套设备使用多少年,可使年平均利润最大?并求出年平均利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com